Originally published in University of California Publications in Psychology, Volume 3(5), pages 215-23, 1928.
Truman, Stanley R. and Wever, E.G.
In the measurement of sensitivity by the Method of Constant Stimuli, it has frequently been shown that a judgment is not simply and invariably a comparison of one magnitude with a standard magnitude, but it may, under some circumstances at least, involve what have been called absolute factors. A given weight may be judged "heavier" by virtue of an absolute impression of heaviness., and not because it is perceived to be heavier than the standard weight that preceded it.[1] The standand, presumably, could have been omitted. Indeed, as work in esthetics, affection, and other fields has shown, a method of absolute judgment may be employed in which there is no standard stimulus, but selected stimuli are presented one by one, and the O reports by absolute impression upon each of them. By such a procedure color stimuli may be judged as to their pleasantness, a set of photographs may be ranked as to their esthetic value, etc.[2]
The Method of Absolute Judgment seems to have arisen quite unobtrusively and without any burden of formulated theory upon it. Yet it is apparent that any given judgment is "absolute" only in the sense of being referred to no particular standard stimulus; it is ‘‘relative'' to some broad and general basis established in previous experience. The experience may be very general and undefined, as when one considers the artistic value of a painting, or it may be mainly restricted to a presented series of stimuli, as is true for a set of colors that are given to be ranked in order of pleasantness.
In the case in which the basis for judgment may be considered as essentially a function of a particular series of stimuli one can study it in its course of development and determine how readily it may be established and become effective for judgment. Such a study is the object of the present experiment; judgment of auditory pitch are considered as a function of a presented series, and the attempt is made to determine how soon one can set up an absolute basis for judgment.
Now perhaps the most direct way of attacking a problem such as this would be to select a set of stimuli, in this instance pitch values, and to present at random the various members to the O until he became sufficiently familiar with the total range to judge them individually in any desired terms, say "high" and "low"; and the number of presentations necessary to establish a familiarity sufficient for report might be a measure of the readiness with which the judgmental level had been established. But here is a difficulty, for, since one must trust the O to decide when he is to begin judging, the situation involves not only the establishment of a judgmental level, but also of a certain uncontrollable degree of faith of the O that the level is adequate.
To avoid this difficulty one can resort to a stratagem: the O is given a standard and is instructed to hold this standard in memory and to render comparative judgments on each of the single stimuli which follow; but the experiment is extended beyond any capacity of memory under the conditions, and hence the O ultimately is forced to an absolute basis for his report The problem remains merely to diagnose when relative judgment has decayed and absolute judgment has set in. Here two ways are open: (1) One might presume that the variability of the judgments would be different for absolute and for relative; or (2) one might choose the standard so that the distribution of judgments on a relative basis would not correspond with the distribution on an absolute basis. In the present experiment both methods have been followed, as will soon be clear.
A. First procedure.—With a Stern Tonvariator a standard tone of 520 d.v. per see, was sounded, and then, by the Method of Constant Stimuli, the O was asked to judge each of five comparison tones, say, 516, 518, 520, 522, and 524 d.v. per see., presented singly in haphazard order. The standard was given twice for two seconds each, at the beginning, and was not again sounded, as standard, until 50 judgments (i.e., 10 series, each with 5 stimuli) had been rendered. These 50 judgments constitute a group called an "A group").
B. Second procedure.—After every even-numbered group of the first procedure a new group was interpolated in which the procedure was exactly the same except that the stimuli of the series were no longer symmetrical about the standard, but were displaced toward the "higher" side; whereas, e.g., a "normal" series (series A) was made up of tones 516, 518, 520, 522 and 524 d.v. per see., with 520 as the standard, the new series (series B) was! made up of tones 520, 522, 524, 526, and 528, with 520 still as the standard. (O was of course kept in entire ignorance of these series, and not once did he show evidence of suspecting a change in the stimuli used.)
Now, presumably, in the first procedure the O at the beginning would make relative judgments, but with the fading of memory for the standard he would be reduced to an absolute basis for his report. And it seemed reasonable to assume that the absolute basis would give a distribution of judgments which approached more closely the order of chance, and hence an examination of the fractionated data of the groups should disclose a decrease in the precision of the psychometric functions as a consequence of the change from relative to absolute. In the second procedure it is plain that if the judgments are a function of the series their distribution must be markedly different in the displaced series from what it was in the normal series, and if they are at first relative and then absolute they should show a redistribution coincident with the change.
Observers. The Os were Miss Marjorie Mallon (M), Miss Neva Mallen (N) and Miss Margaret Dill (D). They were quite naive as to psychophysical procedure. Two, M and N, had enjoyed considerable musical training, and one particularly, N, showed unusually good absolute-pitch discrimination when tested on an instrument (piano) with which she was familiar.
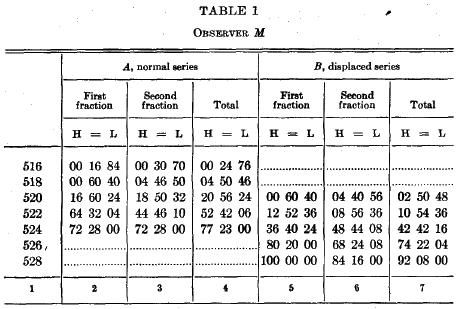
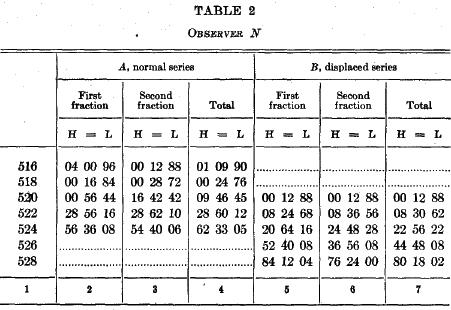
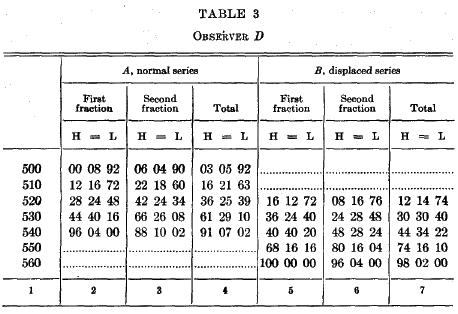
Results. There were five sittings for each O, each sitting involving two groups (A) of the normal series and a third group (B) of the displaced series, making in all 100 series of A and 50 series of B. A rest period of five minutes occurred between successive groups. The groups for each procedure have been fractionated into halves. The first. fraction of A includes the first 5 series of every odd-numbered A group, i.e., the first 5 series of each sitting, while the second fraction includes the last 5 series of every A group. The first fraction of B includes the first 5 series of every B group, and the seeond fraction, the last 5. In tables 1-3 are shown, for each 0, the percentages of judgments of "higher," "equal," and "lower" for every fraction and for the total series of the two groups. The arrangement of the three tables is similar. The columnar divisions are numbered at the foot of the table from 1 to 7. The first division shows the stimulus values used. The second division shows the percentages of judgments in the three classes ("H" higher, "=" equal, "L" lower), rendered for the first fraction of the normal groups, the third division shows these percentages for the second fraction, and the fourth division shows the percentages for all the A series taken together. Similarly, division 5 gives the percentages for the first fraction of the B groups. division 6 for the second fraction, and division 7 for the whole of the B series.

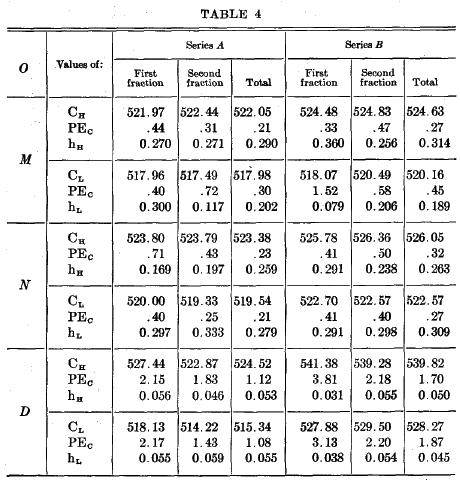
To facilitate the further consideration of the results they have been subjected to statistical treatment. Ogive curves have been fitted, by Urban's method[4], to the distributions of "higher" and "lower" judgments in each division of tables 1-3. For every 0, the values of C, the 50 per cent crossing-points of the fitted curves, of PEG, the probable error of C, and of h, the measure of precision of the curves, have been computed for both "higher" and "lower" distributions, and are shown in table 4. The first column of this table gives the initial of the 0. The second column designates the three above-mentioned values, which bear subscripts (H or L) to indicate whether the distribution is of the "higher" or "lower" judgments. The probable error of each C will be found immediately below it.[5] The last six columns of the table correspond to the six divisions of the data as given in tables 1-3[6].
Discussion. One must first justify the method that has been adopted in this experiment by proving that the conditions do not permit the retention of the standard and, hence, relative judgment throughout the group. Such proof is evident in tables 1-3 in the distributions of the judgments in the B groups. The distributions are not decidedly skewed to one side of the standard (i.e., they are not. predominantly judgments of "higher") as they ought to be if they were relative judgments; they tend, instead, to be symmetrical about the midpoints of their own series, which should be the case if they were purely or predominantly absolute.[7] The differences between the distributions of A and B form a measure of the predominance of the absolute factor; these differences can be expressed most conveniently as differences between the crossing-points of the fitted curves, as shown in table 4, columns 5 and 8. In every case the values of C in B show a shift toward the "higher" side; the shifts are highly significant in every instance, being from 4 to 9 times their probable errors. This is sufficient proof that the absolute factor has asserted itself in the determination of the judgments.
If in the A groups the judgments are first relative and then become absolute, one would not expect any significant change in the values of C in the first fraction and in the second; this is the case; but one might expect. under the conditions, as has been stated above, a change in the values of h. But there is no such change of any significance (compare columns 3 and 4 in table 4); out of the six cases shown, h increases as often as it decreases; and, as has been found mathematically, in but one instance is the difference over twice its probable error. And what is perhaps of even greater import, there are no significant differences in the h. values between the two fractions of B, where a change from relative to absolute, involving, obviously, a redistribution of the judgments, would be expected to cause a marked reduction in the precision of the curves. Nor are there in the C values any significant differences between the two fractions of B, where a change in the basis of judgment would most likely be reflected.
That none of these changes is revealed is taken to signify that almost from the beginning of each group the judgments have been rendered predominantly or wholly on an absolute basis. The results show that the absolute basis for judgment is established with striking readiness and effectiveness; it appears early enough completely tp obscure, within the limits of these observations, any effect of holding over the standard for relative judgment.
The influence of the relative factor in the earliest series has not been revealed in the above results, but this fact does not, of course, signify that it was never present in the judgmental situation; the first judgment most assuredly was a relative one, and it is probable that the relative factor was of considerable importance in the whole first series (of five judgments). With so few groups a further fractionation, as into single series, gives results of little reliability, but such a treatment of the data of the B series indicates, a shift in the distribution of judgments between the first and the second or third series, but no particular change after that. Here, of course, the absolute factor was working against the relative (if the relative was present), and perhaps also against the absolute basis that had been set up by the presentation just previously of twenty series in the A arrangement (It will be recalled that an interval of five minutes separated the two groups). That under these conditions a few presentations sufficed to establish a new judgmental level with such firmness that, for the number of groups considered, the first five series is indistinguishable in the mass from the next five, suggests a remarkable facility for change in the absolute basis for judgment.
Summary. Judgments of pitch may be made on an absolute basis, a basis which has become established by the presentation in haphazard order of the members of a series of pitch stimuli. The establishment of such a judgmental basis is a very rapid process, being probably complete after but two or three series of five stimuli each.
1. See Martin, L. J., and Muller, G. E., Zszr Analyse der Untersehiedsempftndlichkeit (Leipzig, 1899), pp. 43 if.
2. Jonas Cohn describes a later form of the method in his article, ‘‘Gefühlston und Siittigung der Farben," Phil. Stud., vol. 15 (1900), pp. 281ff.
4. For the method, see E.O. Boring, ‘‘Urban's tables, and the Method of Constant Stimuli," Am. Jour. Pspchol., vol. 28 (1917), pp. 280—293.
5. C is what is called the lisnen, L, in the Constant process as used for the determination of absolute thresholds; see note 4, .eupra. The PB of C has been determined by the usual formula for the median of a normal distribution, using the number of series as a. See Ouller, E., "Studies in Psychometric Theory,'' Psyohol. Monog., vol. 35 (1926), pp. 85ff. A value obtained by this method is weighted with assumptions, and must be used with a certain reserve. But as a rough measure it is good enough.
6. The use of Urban's method is justified, of course, only when the data are distributed ‘‘normally,'' or very nearly so. The goodness of fit of the ogives to the observations has been determined for both the "higher" and ‘‘lower'' curves for the total series of A and B, and the determinations are given in table 5; the method of determining goodness of fit follows Thomson (Brown, W., and Thomson, O., Essentials of Mental Measurement (1925), pp. 78-81), who has adapted Pearson's method to the Constant process. The values of P as here determined are unusually high, indicating good approximation to "normality." The distributions for the fractions of A and B diverged, in general, more widely.
7. In regard to the tendency for judgments to distribute
themselves symmetrically about the midpoint of a series, ef. the findings of IL
L.Hollingworth on the estimation of magnitudes (‘‘The Inaccuracy of Movement,''
Arch. Psychol., vol. 2 (1909), pp. 21-39; ‘‘The Gentral Tendency of Judgment,"
Jour. Phil., vol. 7 (1910), pp. 461-469).