Acoustic Learning,
Inc.
Absolute Pitch research, ear training and more
I finally know why I'm having such trouble identifying pitches inside thirds. It's not because I'm not able to hear the pitches-- I can do that just fine. It's not even that I can't hear the individual identities of the pitches-- I can do that as well. The problem, it seems, is my lack of tonal center.
One night last week, I sat down to name individual notes (C-F), and almost casually got 20 in a row without missing a one. I didn't have to work at it, I didn't have to think about it; I just knew them all. It was as simple as reading words out of a book. The next day, I was encouraged enough to try naming major and minor thirds again, but I was just as confused as I ever was before by those pairs that all sounded the same. And then, when I came back to naming C-F, I no longer had the facility that I'd enjoyed previously. I was back to the same process of listening and concentrating.
Now that I've looked at Bruce Arnold's One Note Method I'm convinced that the problem isn't merely that all major thirds sound the same. They do, of course, sound the same, but the reason I can't distinguish them is that my tonal center keeps shifting. Arnold bases his relative pitch course on "scale degrees", asserting that a note in the mi position of any scale will have the same sound as a mi from any other scale. So when I'm listening to the major and minor thirds, I'm so loose in my comprehension of tonal center that each note readily tugs me away from a C-major scale, and I can't help but hear do and mi no matter what notes are being played. On that evening when I could so easily identify C through F, I must have been very clear in my tonal center.
If I can just keep from being drawn away from the C-major tonal center, then, I should have a much better time of it.
I was thinking about the throat-singers of Tuva, and how they can create two pitches at once by manipulating overtones. I idly wondered why ordinary singers don't do this... and realized that we do; it's just that we perceive the overtones as language instead of as a musical pitch, with the "throat song" being the perceived fundamental. I'll have to be a little careful to be sure but I seem to recall that throat singers do not sing words. If I'm right, they would not be able to. (update 9/30-- they don't sing words.)
I was trying to figure out, then, why it is that we hear a virtual pitch. Tonight I've begun reading W.A. Mathieu's Harmonic Experience, and he began by describing the overtone series. I hadn't completely understood, until reading it in his book, that each of the overtones is a successive ratio to the fundamental-- 2:1, 3:1, 4:1, etc. I wondered if maybe there was something in the pattern of overtone pitches which made our minds invent a sound that isn't there, but after laying out a bunch of coffee stirrers in place, to represent overtones striking the ear's receptor cells, I was none the wiser. I didn't see anything glaringly absent which would suggest the missing tone.
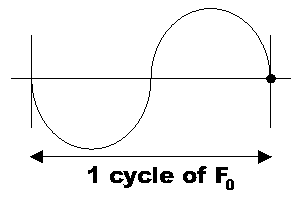
Then it occurred to me that a pitch is perceived by where the basilar membrane strikes the receptor cells most strongly. It also occurred to me that the ear is arranged so that the higher frequencies are on the outer part of the ear-- that is, the further in you go, the lower the pitch. This suggests that the fundamental frequency is the endpoint of the waveform. And, recognizing what Mathieu was describing, I decided to draw a diagram of the fundamental tone

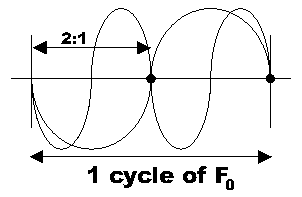
and then added the first overtone,
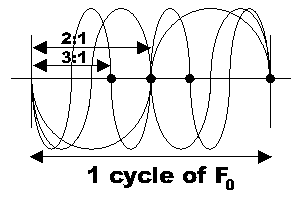
and then the second,
and then took out the fundamental.
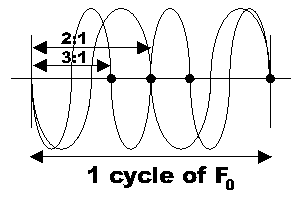
As you can see, because the waves are all in ratios of x:1, they all end up striking the fundamental spot at the same time. That is, there is one spot where the waves do not cancel each other at all, but in fact augment each other more strongly than at any other spot in the cycle. I tested this idea on the sine wave spreadsheet and sure enough, the first three overtones (minus the fundamental) of A440 created a composite wave with a totally recognizable 440Hz frequency.
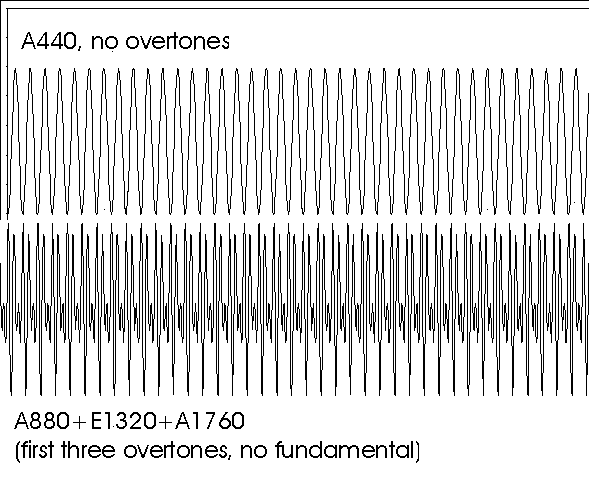
Could it be that the virtual pitch is not invented by the mind's apparent need to hear "what should be there", but instead is literally heard, created by the overtones? It certainly seems possible.
I've been musing about overtones lately. I had to figure out, in the first place, why overtones occur. WA Mathieu takes it for granted that they do occur, and doesn't explain why, even though his entire book is predicated on the overtone series. This isn't a conceit on his part; he just assumes (correctly) that other people have already covered overtones exhaustively. Although Mathieu doesn't explain why the overtone series occurs, he presents an excellent description of its significance to Western music. (He has experience with the music of other cultures, but that's not what I'm looking at right now.) He begins at the end of their descriptive work and takes it much, much further.
I had thought that I would work my way through the entirety of his book before I began critically reading The Psychology of Music, but his warning turns out to be apt. In his introduction he says that you can't just sit down and read; you have to sing and play and listen to the things he's talking about or you will eventually be left scratching your head in puzzlement. And, you know, he's absolutely right. I've read far enough now that I can see what he means but there's a vast disconnect between his words and what I can imagine in my head. So I'll have to proceed in Harmonic Experience more slowly, and take Psychology of Music with me instead when I find myself at a coffeehouse somewhere.
I was at a coffeehouse the other day, lying on a couch, meditating on the overtone series-- trying to imagine why Mathieu was so careful in describing it. It was clear enough how the notes in the overtone series bore mathematical relationships to each other, how then does that series translate to music, I wondered? It hit me quite suddenly, and I sat bolt upright with a short yelp of surprise (the startled fellow sitting near me cautiously moved to a different seat). When a piece of music is "in the key of x", that means that we hear all of the notes in the piece in terms of their respective consonances and dissonances to the overtone series of the base note x. The "good" notes are the ones which reinforce the overtones, and the "bad" notes are the ones which conflict and cause "roughness". Once I'd thought of this, it seemed far too obvious not to be common knowledge, and I did indeed confirm the fact with my composer friend as a basic concept in musical training.
Mathieu cautions that "we don't hear harmony simply by matching overtones", but in saying so he's not contradicting the basic idea of key signature, but introducing a new issue of psychological response. In fact, with the overtone series, whether he intended to or not, Mathieu has also clearly explained some points about perfect pitch which have been dogging me terribly.
It seemed from Miyazaki's experiments that people with perfect pitch did not hear intervals directly, but inferred them from the component notes. IronMan Mike, who has absolute pitch confirmed that each "interval" is, to him, twelve different sounds instead of just one. But when I suggested that perhaps he (and other people with AP) learned intervals like mathematical tables, gradually learning that these twelve are "minor third", these twelve are "perfect fifth", etc, he disagreed, assuring me that each type of interval definitely has some common sound. This was a maddening statement-- if people with AP are able to hear a common sound in an interval, why then would they have such difficulty with transposition, and have to develop strategies to make it possible for themselves to accomplish transposition?
Mathieu has solved the problem by showing a distinct difference between the harmonic relationship of notes and the melodic relationship. He sets you up, pointing out that the frequency ratio of an octave's notes are 2:1, and that the octave is the eighth note on the scale; then he knocks you down.
So is an octave a "two" or an "eight"? It is clear that the harmonic name, 2:1 (based on frequency ratio), and the interval name, octave (based on scale steps), refer to different aspects of the same thing. The distinction between the names does not seem terribly problematic in this simple case. But in more complex cases the competing nomenclatures create a murk so obfuscating that entire theory classes have been known to return home to mother.
I've been having a grand debate via e-mail with a fellow who is certain that people with absolute pitch must be listening in relative pitch because otherwise, he insists, how could music make any sense to them? This perspective, quoted above, of "different aspects of the same thing" makes clear that AP listeners are attending to the harmonic interaction of notes, rather than the intervallic distance between them-- and if that weren't enough, Mathieu drives the point further home:
Try to appreciate your melody not so much as an up-and-down ride, or even as a series of intervals, but rather as a succession of related harmonic states, a succession of moods. The secret of melody is that it is a thread of feeling-states such as these.
This could be the essence of AP musical listening: harmonic listening. I've described before my impression of how AP listeners must hear musical notes occurring instead of changing. The fellow I've been debating with doesn't think a person can remember a piece of music with complete disregard for what he terms "frequency ratios". Mathieu explains it here quite poetically. When a musical phrase has a C followed by a G, the relative-pitch listener hears five notes up, and the absolute listener hears C, then G. The RP listener hears a relationship between the first and second note; the AP listener hears a new harmonic state.
This is in exact accordance with how IronMan Mike, in his jazz musicianship, has described his strategy for transposing. He takes the component notes, identifies their interval, transposes the letter names to the new interval, and produces the notes corresponding to the result. Although he recognizes that each interval demonstrates a similar harmonic sound, his mind considers the transposed harmonic state to have an entirely different identity. It simply doesn't make sense to move the notes-- notes don't "move". He needs to select different notes.
[Mike says that he does this almost instantaneously, so that no one would ever guess there's this four-step process going on in his head. He seems to any observer to have excellent relative pitch. This is the mirror image of relative-pitch listeners who have refined that ability so well that they seem to any observer to have perfect pitch.]
There are two different aspects of music which Mathieu laments are too commonly mistaken to be essentially the same thing-- harmony and melody. You need to learn the difference between harmonic and melodic relationships. This is the difference between frequency ratios (absolute note interaction) and scale degrees (overtone reinforcement). You need to know both types of listening. If you learn the sound of the "interval" you have only learned part of the story. Curiously, someone with perfect pitch may only be getting part of the story, if they do not know the sound of the interval! Do they hear the harmonic state instead of the "distance" between the notes?
The challenge becomes, of course, learning to hear both at once.
I'm so excited I could scream.
Yesterday and the day before, I had been corresponding with Peter, who had clued me in to the vowel idea. We were sending voice recordings back and forth, to make sure we knew exactly which vowels we were talking about-- for example, to a continental European, the word spelled "bit" is pronounced the way I'd say "beet". He hears a specific vowel sound for each note; I don't yet hear all of them, so I wanted to be absolutely certain which vowel sounds he thinks correspond to each note. We compiled a list which had written letters representing sounds that we both understood, one for each note of the scale. But that was two nights ago.
While I was driving home from a script reading yesterday evening, I was thinking about how the Dutch research page, as well as plenty of other sites, showed how vowel sounds could be clearly heard just by pushing air through a tube that's been cleverly formed to mimic the structure of the mouth. I had downloaded the sounds from the Dutch site, hoping to run them through a spectrum analyzer, because they could show me what vowel sounds looked like with only formants (and no fundamental pitch). But then, as I thought about the sound of those files, I realized that I could make the sounds myself-- by whispering. If I whisper, my vocal cords don't move, and therefore there is no fundamental pitch-- only the formants created by the shape of my mouth!
In the car, I shut off the CD I was playing and began huffing vowel sounds. I was fascinated by the fact that I couldn't whisper a vowel sound at different pitches; each time I'd try to change the pitch, the vowel sound changed right along with it. I tried to whisper the same vowel an octave up or down, but I couldn't quite manage it due to lack of practice.
...Lack of practice, you ask?
I hadn't realized before that the reason the formants don't change when you change the fundamental pitch-- a fact I had read in my research-- is because the way you shape your mouth doesn't change. Try it-- say any vowel at all. Now hold your mouth in exactly that position and let your vocal cords produce different (fundamental) pitches. You can range that fundamental pitch anywhere you want with your vocal cords, and keep the vowel the same-- because your mouth's shape doesn't change. At all. So when you speak, you say an "a" the exact same way every time, with exactly the same mouth shape. You just don't have any experience saying the same vowel sound in a different part of your mouth! That makes it incredibly difficult to hit the octave shift, then say the "normal" vowel to compare, and then come back to the octave vowel to make sure.
When I got home, I immediately went to my computer and recorded all the vowel sounds in whispers. I was excited to run the recordings through a spectrum analyzer program and compare the overtones of each vowel to the piano tone that Peter said they corresponded with. So I saved the files and loaded the program and...
...and I realized that I hadn't the faintest idea how to interpret a spectrographic display. I was able to figure out how to change the display to a frequency analyzer, but I didn't know how to put the two displays (whisper and piano) together to make a valid comparison. Frustrated, I left it alone for the night.
But today, this afternoon, I had a brainstorm. It struck me in the last hour of the working day and I could barely sit still for my excitement to come try it out. I picked up the thesis on my way home, rushed in the door, snatched the Suzuki Volume One book off the shelf, and sat down at the computer with my vowel-whispering files and a copy of the list that Peter and I had put together.
And this is what I did.
This isn't a piece of music-- it's me whispering vowels that have been cut-n-pasted together using Cool Edit Pro. The song is sol mi mi, fa re re, do re mi fa sol sol sol, sol mi mi mi fa re re re do mi sol sol mi mi mi. If you've taken Suzuki training, you'll recognize it as "Lightly Row".
I used this guide to do the cutting and pasting (my accent is "neutral" Midwestern).
C = o as in board
C# = o as in boat
D = u as in but
Eb = o as in boot
E = a as in balk
F = a as in father
F# = a as in bake
G = i as in bit
Ab = u as in burn
A = i as in time
Bb = e as in beet
B = e as in bet
and you can hear the results for yourself. If you want to hear the vowel sounds more clearly here is the stretched version of the file.
Remember, I recorded the vowels last night, before I had the idea to cut and paste them together. I recorded them as vowel sounds and made no attempt to speak them at any particular pitches. (The tricky one is the "i" sound as in "time", because "i" is a diphthong. The vowel sound you want is the "aah"-ish sound that is the first half of the "i".)
Although Peter says this list of vowels is accurate, and I have heard a few of them myself on the piano (the F/F# a-vowels are particularly clear), the whispered vowels don't seem to correspond to the pitches above absolutely. But they clearly correspond relatively.
And the best thing about this recording is that YOU CAN DO IT YOURSELF. You don't have to take my word for it! In whatever sound-recording software you use, just record yourself whispering each of these vowels; then find a piece of simple sheet music and cut-n-paste the melody together using your vowels. Please let me know if you get any unexpected result!
I've begun reading the University of Calgary study. I have finally learned, from this study, how it was that PT Brady taught himself "perfect pitch", and his method was really quite simple. He drilled individual pitches from the chromatic scale, using all pitches but with an overabundance of C notes, and when he was able to identify the C consistently and flawlessly he dropped the overemphasis and drilled all the notes equally. These kinds of exercises you can construct for yourself using Nathan Becker's Tone Quiz. I'd need to read more about how and what Brady was able to hear after achieving his feat, but I think that the standard he was held to in his achievement was that of "being able to identify or recall any note without a reference"-- the standard definition of absolute pitch. When "tested" in this ability, he "scored" at levels comparable to people who had naturally-occurring AP.
What I don't know is whether or not he actually learned to hear in perfect pitch. Did he learn to recognize the inherent quality of a sound, or was he able to hear a sound and relate it to his knowledge of musical pitch? This is not merely a semantic distinction. Any sound we experience is a container for pitch just as surely as any sight we experience is a container for color. A stoplight does not create red; it is red. A coin dropped on the counter does not create a pitch; it must be a pitch. Hearing the coin drop and simply knowing its pitch-- without even having to recognize the association between the sound and its pitch name-- is vastly different between hearing the sound, reflecting for a moment (even if only a fraction of a second), and identifying "yes, that is the same sound as a musical F".
What the genetic researchers seem to overlook... and I can speak more confidently of this now that I've actually received this reply from one:
"...the bottom line is that people simply learn to associate a sound (pitch) with the name of a note by musical training. if one isn't exposed to the scale, then one can't be expected to develop "perfect" pitch."
...is that the notes of the musical scale have nothing to do with perfect pitch. The musical scale is simply the answer to the perplexity of, how can you describe the quality of a sound? How do you linguistically code your meaning so that someone else will understand? Ultimately, what words can you possibly use-- except for the notes of the musical scale?
Now, literally, I don't disagree with the statement I just quoted, not at all. People do learn through musical training to associate a pitch with the name of the note. Also, if one is not exposed to the musical scale, one can not be expected to develop perfect pitch. But for those people who already have perfect pitch, and do not need to develop it, the musical scale is irrelevant except as a device with which to categorize and describe their experience.
So what are they hearing that the rest of us are not? It seems that they are registering the specific frequency information of any given sound in addition to its intellectual interpretation as a "musical note" or "air horn" or "door slam" or any other representation you can conceive. Daniel Levitin puzzles explicitly that "absolute pitch information is available" at many stages of the mental process, so why don't we all hear and comprehend it? I suspect it may be because we have become habituated to the raw sensation of sound, since we learn (especially in music) that sounds are to be interpreted rather than experienced.
This is why I'm so keen on the vowel-pitch association theory-- because, potentially, it presents a non-musical way to listen to the inherent qualities of a sound, and in a way that we already know how to listen (as opposed to "pitch color", which must be understood before it can be heard).
Why can we recognize an "s" the instant we hear it? Why do we know the sound of an "a" without a moment's hesitation? Why is it that instantaneous recognition of musical pitches is recognized as some phenomenal ability, when the very fact that we can make sense of speech is testament to our natural ability to instantly comprehend sound information?
Rationally, logically, the idea of vowels as pitches is very appealing. There's plenty of evidence to suggest it, biologically, linguistically, and musically, an adequate part of which I've documented. And learning perfect pitch, therefore, would become merely a matter of sensitizing yourself to the subtle sound of a particular vowel and then hearing that vowel sound wherever it occurs in nature. It's very compelling to imagine that the formant series of a linguistic sound is akin to the overtone series of a musical note, and that the formants thereby make us hear a missing fundamental pitch which is then recognized as the basic vowel sound.
There's only one problem with that-- whispered vowel pitches vary from speaker to speaker. When the fundamental tone is removed (either with a computer, as in this link, or organically, which you can do yourself by whispering), the vowel has a distinct and invariant pitch-- but that absolute pitch is dependent on the length of the vocal tract ("buislengte" in Dutch). I learned from my own demonstration that the chromatic scale represented by vowels is going to be relatively the same for each speaker, but absolutely they're definitely different.
So how do we understand vowels? Do we learn to recognize them "instantly" in the same way that someone with musical relative pitch "instantly" recognizes the complex sound of an interval? Or do we recognize vowels instantly because they imply the virtual pitches from which they were conceived? I wanted to believe the latter, especially since there is the study which compellingly shows that the fundamental pitch is more important to the sound than are the formants. On the piano I can clearly hear the "a" sound of the F#, but when I whisper that vowel its formants create a virtual A#-- and when someone else whispers that "a" sound, it creates a different pitch.
There's a fellow named David Alan Stern who has a series of tapes called "Acting with an Accent". He says, in each tape, that your principal task is to speak with the "resonance" of the accent; once you have achieved this, he says, the vowel sounds fall in line and the rest is mechanical detail. When I was contemplating the possibility that spoken formants create the virtual pitch of a specific vowel, it seemed to follow that if you change the basic resonance of your voice you must also change how your mouth forms every vowel, because you have to correct the sound of the fundamental pitch in a different way. And, in fact, I can tell right now as I shift from Irish to British to American resonance that my mouth does change its formants when forming the same vowel, responding to that altered resonance. This must be why people find it difficult to produce accents-- their mouths are so convinced that a vowel's formants must be formed in a certain way that they simply don't understand how an "a" (or whatever vowel) could be spoken in any other configuration. But the formants can change when you change your accent; and, if I discover what I think I will when I whisper them in different accents, I may have to conclude that the fundamental pitch is not being corrected at all, but simply ignored. In fact, as I drove home tonight listening to a CD (Ray Stevens' Everything Is Beautiful), I found it fascinating to listen to the singer and hear the sung pitch and the language sound as entirely separate.
And yet-- I have a fan blowing on me, right now, and its whir is definitely an A (I checked on a piano keyboard). And I can clearly hear the "i" sound that it is producing, just as it should according to the list that Peter and I constructed. So it's surely not the musical overtone series which creates the vowel sound of a note, and it's not necessary to have linguistic formants; the pitches we hear in nature do seem to possess consistent vowel sounds.
Somehow I have to reconcile the fact that the vowel associations are relatively but not absolutely correct in each case of whispered vowels, and I have to figure out why it is, then, that natural pitches are different from linguistic vowels.
I don't think I'll figure it all out tonight.
The fact that the vowel pitches can change from speaker to speaker, depending on the length of their vocal tract and the dialect they speak, makes it seem less likely that we hear vowels because the formants (overtones) of those spoken vowels create a specific virtual pitch which is what identifies the vowel sound. This doesn't mean that virtual pitch should be written off altogether. Clearly the whispered pitches do create a recognizable pitch, and, again, relatively the pitches are correct for this list of vowels. Additionally, Ernst Terhardt describes the "remarkable coincidence" (that is, scientifically unverified observation) that "the auditory system's dominant region for speech intelligibility may be more or less identical with that for the formation of virtual pitch." In fact, if you follow that link, you'll read Terhardt's description of how a telephone line doesn't carry the fundamental frequency of the human voice!
Some of the facts of the case:
Whispered vowels create virtual pitches.
The vowel-pitch associations above appear to be relatively correct when spoken.
The vowel-pitch associations above appear to be absolutely correct when played on the piano.
Absolute virtual pitches vary between speakers, sometimes more than a semitone.
The language sound is separate from the spoken fundamental frequency.
The formants can change completely and remain intelligible.
Peter has taught himself absolute pitch by listening to vowel sounds.
The known formant combinations which comprise vowels have very little overlap.
Ordinary listeners know linguistic sounds instantaneously.
I'll also reiterate my original speculative thought: since absolute pitch is a hearing style, not a musical skill, the AP listener must be responding reflexively to sound before processing it intellectually; they must be listening for something other than "music" when they hear musical sounds.
I can reasonably say at this point that musical tones evoke certain vowel sounds. How or why this should be, I don't yet have a solid idea for. I'll have to shelve this line of inquiry for a while, I think, while I read more from Mathieu and Deutsch. As I learn more I'm bound to speculate more clearly. And if you come up with any shattering insights, by all means, tell me!
Just when I thought I'd had as many revelations as I was going to have for a while, just when I thought I was going to sit back comfortably in my ol' rocking chair and read a while-- to report the findings back to you, of course-- something pops up that blows me away. Again.
Are you familiar with the computer simulation Life? I'd be surprised if you hadn't encountered it by now. No matter if you didn't, of course-- simulated societies have come a long way since then. And that's what I thought I was reading about on Friday, in a fascinating article that I'd been led to by some investigations on economics and profitability. But partway down the page a paragraph began with this quote:
Every so often scientists notice a rule or a regularity that makes no particular sense on its face but seems to hold true nonetheless. One such is a curiosity called Zipf's Law.
Three paragraphs later my eyes were wide and my jaw was on the floor. I immediately looked up as much information about Zipf's Law that I could find. Zipf's law isn't a "law", exactly, in the same way as any ordinary mathematical or physical law. It's a "law" in the same way that Murphy's Law is a "law"-- you can't prove it, you can't explain it, but every time you look, there it is.
Zipf, a scientist who lived in the first half of the 20th century, noted that in a given piece of writing, the most frequently-repeated word (usually "the") tends to appear twice as often as the second-most repeated word. That is, if there are 1200 instances of the word "the", then the second-most common word ("of", perhaps) will probably occur approximately 600 times. And then the third most frequently-used word (maybe "to") will show up one-third as often, which would make it in this example about 400 times. That observation in itself is curiously remarkable-- and if it were only applicable to language, then it might remain merely a curiosity. But this same law applies to city sizes-- the largest city is twice as populous as the second largest, and three times as much so as the third largest, and so on down the line. The law shows itself in the size of corporations, in random distributions, even in Web traffic-- it's eerie. For each successive iteration, Zapf's law observes a ratio first of 2:1, then 3:1, then 4:1 and 5:1 and...
...starting to sound familiar?
I know I've got perfect pitch on the brain-- everything I read and everything I think about tends to be filtered through that lens, because I never know what's going to be relevant. But to find that populations of cities and sizes of corporations bear a natural similarity to the overtone series is absolutely unbelievable! Of course, Zipf's law seems to be backwards in this context-- the overtones are overtones because the first-ranked note, the fundamental pitch, has a lower frequency than the others, and the ratio 1:2 means that the second-ranked note is actually twice the frequency of the first, not half (like the second-ranked city's population would be). But backwards or forwards, there it is. [Update 8/12/3 - Sean has written to point out, "If you consider the ratios of the wavelengths of the sound instead of frequencies, then they should match with the order of Zipf's law. That would be the better comparison."]
I was rather shocked to see that there doesn't seem to be any inquiry at all into how Zipf's law applies to the overtone series in music. Maybe it's too obvious-- after all, what would such a study prove or examine except that which is already self-evident? You'd have to be a very clever scientist indeed to relate acoustic frequencies to any other known Zipf phenomena... or perhaps not quite so clever-- there must be many more examples than the half-dozen that I've now read about, and some of them might be directly relevant. Nonetheless, it was amazing to me that I could find one and only one study about Zipf and music. And even then, this study doesn't attempt to address the natural overtone series, but attempts instead to analyze the frequency of occurrence of notes within music.
I must admit, I wonder how much these mathematicians know about music. They're congratulating themselves for finding "Zipfian distributions" in great classical compositions. But even with what little I yet know about musical composition (I'm a performer, not a composer) I could've told them that in a truly well-written piece of music that they could expect nothing else! Think about it-- one note occurs with the greatest regularity. Then another note occurs half as frequently. A third note appears one third as often. At risk of sounding a bit unscientific let me say, well, duh! That's what's called "staying in key". Unless I've misunderstood what I've been reading, a composition will consistently reinforce the key that it's in by proportionately large emphasis on the base note, with the most harmonious partials then receiving favored treatment over dissonant notes. Well-written music is designed to follow a "Zipfian distribution"! The scientists say that their next step is to see if they can write a computer program to generate random musical tones following a Zipfian distribution. I dare say that they'll discover the very simple fact that all the computer has to do is generate a random melody in key.
I'd go so far as to say that what they should be doing is not to analyze music to see if it exhibits the distribution-- of course it does!-- but why on earth music developed so that the "Zipfian distribution" became a necessary and natural component of it. Now that would make for interesting reading.
I do confess that that's too big a topic for me (right now)-- for now I'll be content to look at the music of Zipf's findings in wondrous awe.
At this point, my completely unverifiable theory (predicated on the legitimacy of the theory of evolution) is that pre-human animals, lacking the mouth structures for linguistic facility, were originally able to make pitch noises to communicate. As mouth structure evolved, I suspect that the comprehension of linguistic sounds shifted from being pure pitches, formed only by the throat, to being virtual pitches formed by the mouth. Recognizable phonemes then evolved-- developing out of ranges of single pitches into acceptable ranges of complex sounds. Some circumstantial evidence for that idea appears in the fact that older languages, like Japanese, have more precise vowel sounds than newer languages.
It doesn't necessarily follow that a linguistic sound will always produce the same pitch-- and I've shown that it won't, with those whisper recordings-- but it does seem probable that the ordinary acoustic phenomenon of each musical tone must fall within the same acceptable range as a specific spoken sound which we have learned (in other contexts) to recognize linguistically. I'll explain further.
Peter had taught himself perfect pitch by listening for vowel sounds, and his description of his new style of hearing was extremely similar to what I'd learned about natural perfect-pitch listening (from perfect pitch listeners describing their experience). He said that when he listened in "perfect pitch mode", he lost the sense of the melody in favor of a succession of unconnected notes. The notes were not moving up or down, they were simply occurring one after the other. This was precisely the type of pitch perception described of toddler musicians by the Suzuki violin teacher whom I spoke with.
I had speculated, therefore, that the single frequency of the pitch itself was what he was hearing as the vowel sound. Perhaps, I thought, spoken vowels create a specific virtual pitch and we recognize that as our linguistic vowel. After discovering that the whisper-sounds produced different pitches from what I could clearly hear myself on the piano, I had to revise that idea; if the vowel sound were a consistent pitch then the virtual pitch created by the whisper-pitches would surely be the same no matter what. I had to go back and look at what makes a vowel sound.
"Formant" combinations define vowel sounds. The "formants" of vocal speech are extra pitches added to the sound of your voice. These pitches are determined by the way you shape your mouth; their frequencies are separate from fundamental pitch of your voice. You can speak or sing any pitch you want to, and as long as the formants remain the same, your listener will hear the linguistic sound you intend. Specific F1 and F2 formant combinations, where F0 is the ignored fundamental tone, define specific vowel sounds. (I know I've discovered that this simple F1-F2 definition isn't the entire story, but it is nonetheless demonstrably true.)
Look at the chart, and notice that although each formant combination spans a range of frequencies, there is almost no overlap between them. Each pair of formant frequencies forms a very specific vowel. Where there is that small overlap between ranges, I suspect you would hear an indistinct vowel which could be taken for either one depending on the context (it's not surprising that the range with the most overlap is the neutral schwa). So when you play a musical note, it seems possible that the overtones of the musical pitch create frequency combinations which fall directly into one of these ranges and, therefore, can be clearly recognized as a specific vowel sound.
In short: the same vowel sometimes produces different pitches, because its formant combinations can fall anywhere within its entire range (to produce a different virtual pitch); but a musical pitch always produces the same vowel sound, because it always falls within the same vowel range.
Why bother with vowel sounds, then? Peter's experience leads me to conclude two critical benefits from listening for vowel sounds-- two factors which are essential to your ultimately hearing in "perfect pitch mode". One factor is that you will not be expecting the notes to be higher or lower than each other. You will simply hear them as different. After all, you don't think of a U sound as "higher" or "lower" than an O, do you! Another factor is that you will begin to hear the notes occurring instead of changing.
This is a subtle but incredibly important point. It may help to make an example with language. If you say a word, "dog" (for example), you wouldn't say that the "d" sound changed to the "o" sound which then changed to the "g" sound. You'd say that the "d" was followed by the "o" and the "g". They're three entirely separate sounds. So when you hear a C# and then a D, you wouldn't say that the C# had moved up a half-step; you'd say that the C# was followed by a D. You may happen to know that it's a "half-step higher", but that information is irrelevant.
When you do perfect pitch exercises, don't try to hear the vowel sounds at the same time you're trying to hear the more sensory characteristics of the pitches. They don't go together well. Do an entire exercise one way and then do the entire exercise the other way. Ultimately they may fuse together (Peter says he's achieved a kind of "3-D listening") but the two modes do not seem to be compatible initially.
Thanks to inter-library loan, I have been able to read the research performed in 1991 by Marguerite Nering for her master's thesis at the University of Calgary. I'd encourage you to visit your local library and borrow it yourself-- the research and analysis is preceded by a fairly exhaustive treatment of the basic concepts of pitch and absolute pitch, presented thematically (instead of chronologically, as I've been doing). While you're waiting for it to arrive, I'll take some time to look through it and tell you what you've been missing.
Nering's abstract makes clear that her study is intended to test Burge's "methods"; furthermore, she explains that her scientific determination of successful learning is based on the standards that Burge himself has set. I found myself wondering if Burge had actively recruited Nering to create an academic treatment which he could use in his advertising. Although that doesn't seem likely, the study results are analyzed only according to Burge's definition of perfect pitch-- so in essence, the study asks "Does Burge's product do what he says it does?" and not "Does Burge's product teach absolute pitch ability?"
The study itself is simply constructed. Nering recruited seventy-eight undergraduate music students to participate, all of whom were enrolled in conventional ear-training courses at the school. She developed a test for note identification and administered this test to all participants at the beginning and end of a single semester. Thirty-three of the subjects received no ear training other than the ordinary Calgary curriculum, and the other forty-five practiced perfect-pitch exercises every day. In such a short time frame, she didn't expect anyone to develop full perfect pitch-- her resolution was that those who trained with the perfect-pitch exercises (the experimental group) would not fully develop the ability, but would nonetheless show recognizable improvement in test scores where the control group (who did no extra training) would stay the same.
And, indeed, that's just what she discovered. On every test, in every category, the experimental subjects showed results in the final test which had improved from the pretest, and the control subjects demonstrated "no statistically significant improvement". Her abstract concludes, therefore, that perfect pitch exercises are effective in improving pitch discrimination.
This does not surprise me-- I know my ability has been improved, and if you've been doing similar exercises then so has yours. It also doesn't surprise me that she should have achieved statistically significant results in such a short time; once you know how to listen and what to pay attention to, you immediately have an advantage over listeners who aren't sure how to identify a pitch. Developing full and automatic pitch discrimination, of course, takes considerably longer; once you get over the first hurdle you'll be delighted with your leap forward, but after that it's a doggedly incremental effort of reinforcement, reinforcement, reinforcement. Later in her publication, Nering speculates that full perfect pitch ability should develop through two years of uninterrupted effort, practicing for at least half an hour every day without missing even one day. (Once I reach that page I'll quote it directly, but I thought you might want to know it now.)
In that respect, yes, the study only says that after four months, you'll be better at naming notes. But the wealth of essential background material that she supplies should provide many interesting thoughts and additional context for the other books which I also look forward to sharing with you.
In Marguerite Nering's introduction, there's one statement which I definitely agree with, and which can certainly be suggested as the primary purpose of my website: "[Currently] almost the entire emphasis of [ear training] courses is placed on relative pitch abilities. Perfect pitch training, if effective, should become an integral part of these courses."
It seems that the main reason why so few people have acquired perfect pitch is because they never tried, and the reason they never tried is that they never knew they could try. I was certainly amazed when, last year, I was made to realize that I'd simply always assumed that perfect pitch was inborn, without even having a good reason for my assumption. I also learned to whistle this year-- I'd never been shown how, and now that I've learned, I'm so delighted to be able to that I've been annoying my co-workers for months with various tunes. When I mentioned to my voice teacher that I'd just learned to whistle she immediately expressed great surprise, saying that she'd always assumed that whistling was a born-with ability. Considering her substantial musical credentials, and the superior physical technique she exercises and teaches in singing, it's certainly remarkable that she would have settled for such a conclusion! But she did do so, and never thought much further of it. It's not exactly easy to learn to whistle; I suspect that I learned quickly because I pick up dialects well, so I'm accustomed to mimicking the shape of others' mouths as they produce noise. All I needed was a model to work from, and now I'm warbling like anything. (I find this encouraging mainly because now if I ever land the role of Sweeney Todd I can perform the song Pretty Women.)
It's even harder than whistling, of course, to learn or teach perfect pitch. Whistling, as difficult as it may be to learn, can still be visibly modeled. It was strange trying to explain how I changed the pitch of the whistling-- I just started doing it, without knowing how-- but I was able to observe my lips in a mirror and draw meaningful conclusions from those observations. With perfect-pitch listening, obviously, you can't observe anything directly. You have to create your approach from what you think perfect pitch is; the more you learn about the phenomenon, the more clever you can become in attacking the problem.
I think it's a terrible shame that children aren't taught their pitches as they're taught their colors. There's a fellow who has developed some musical composition courses for young children, which are also effective for adults-- he makes the salient point that when we're young we're encouraged to paint and to write, but not to compose music. If perfect pitch is something which can be learned right along with other artistic skills, then Nering is absolutely right-- the world community should know about it; the world's schools should know how to train for perfect pitch.
Nering's hypotheses are appropriately simple. She asserts that if the University of Calgary students do their perfect-pitch exercises, that their perfect pitch ability will be "improved or attained" at three levels: pitch discrimination on their own instrument, pitch discrimination on any instrument, and aural recall. She furthermore states that if the exercises are no good, then no improvement will be demonstrated. Considering that the point of the thesis is to find out whether or not the exercises "work", there's certainly no more succinct way to put it!
More interesting are the few limitations of the experiment which she describes.
I feel obliged to point out that she defines absolute pitch as "the ability to identify or produce a specific tone without benefit of a previous reference", and that she makes a distinction between "passive" and "active" absolute pitch which my studies have suggested may be a misleading perspective.
Importantly, the subjects were tested only on single tones. If you've been doing perfect-pitch exercises you've discovered how different it is attempting to identify notes all by themselves versus recognizing them when they're mixed together in chords and arpeggios (notes played in sequence). In my experience so far, recognizing single tones is much easier. This could, I suspect, affect Nering's study to the extent that her subjects would be more likely to show significant improvement in their single-pitch abilities.
Although she says that no one is tested on relative pitch, there's no indication in the introduction that she's going to attempt to prevent anyone from using their relative pitch-- the old perplexity that once you begin a test, the first note is a reference, and anything following can be intuited from that first note if you already have strong relative pitch. In a learning situation, this is not a problem, but in a testing situation, it can confuse the results. We'll see later if there's any accounting for that effect.
The only other limitation which she explicitly states is that she had no control over whether or not the participating students actually performed the exercises with the necessary rigor. The students were asked to do the exercises on their own, with partners, outside of the experimental setting; although they kept logs of their attendance and their efforts, and although they were told that their perfect-pitch ear training "would not be marked" as part of their regular classwork, Nering speculates that some students may have overstated their involvement for fear of harming their class grade, and she says flatly that some students did not fully participate due to conflicts with their partners. The most likely effect of this lack of dedicated exercise is, of course, that the students who claimed to exercise would show no improved ability and therefore make it seem as though the exercises were ineffective. Presumably, the quantity of participants would minimize this effect, but if the results seemed to show a variability from subject to subject then it introduces the question of whether perfect pitch can be learned, using these exercises, only by people who already have a talent for it and not by those who don't.
But we'll see.
I was delightfully surprised today to receive some very interesting and informative questions in my inbox. One of them relates directly to the next part of the Nering study:
I´ve read in the board that there are different kinds of PP, and they're called by number I think (ap1, ap2, etc). I know that it has to do with the quantities of timbres you can hear, the extension, the amount of pitches, etc, but I don't know what are the exact differences between each kind. Could you tell me what they are? - Emilio
There seems to be no chart of perfect-pitch ability level which is generally accepted-- at least, I haven't encountered one, and I haven't seen any serious research that even attempts to refer to specifically numbered levels of ability. Some people will refer to "AP1" as the most complete level of musical note recognition and recall, but there is no meaningful and universal assignment of "AP2" or 3 or so on.
Nonetheless, Nering has done us the favor of naming six manifestations of absolute pitch ability:
1 - "the subject notices but is unable to identify the tone color"
2 - "the subject recognizes the notes on his or her primary instrument"
3 - "the subject is to detect sharpness or flatness of a tone on his or her
primary instrument"
4 - "the ability to discriminate between the twelve tones on any musical
instrument"
5 - "the subject is to detect sharpness or flatness of a tone on any instrument"
6 - "ability to aurally recall any of the twelve semitones.. with no objective
reference"
I wince, as usual, at the term "tone color" for "pitch", but again, there's no better word (yet). Notice, as you look at this list, that although they do seem to describe an increasing level of ability, sometimes the boundaries between these levels are muddied; sometimes a person can develop strong aural recall which is wholly dependent on their own instrument. I was intrigued by this comment I received earlier today:
I think your website and your ideas about the nature of perfect pitch are fascinating, and I am extremely interested in developing this skill. I want to tell you about my situation, and ask your advice on "what it means" and how I should proceed from here.
I am a music major, and my primary instrument is the tuba which I've been playing for about 9 years. As a warm up routine, brass players often work chromatically down through the partials of their instrument to get their lips buzzing comfortably. This always begins on our "tuning note" - which uses no valves - and is a Bb in the tuba's case. From there, the second valve sounds A, back to Bb - First valve is Ab, back to Bb - Valves one and two is G, back to Bb etc etc. I was thinking about how you were talking about learning the difference between C and D, and began thinking about Bb and A and instinctively fingered the valve combination in my hand. I thought about how Bb is not A - etc and sang out loud what I thought were those pitches. Walked over to the piano and of course, right on the money - Bb and A. Mind you this is without any actual perfect pitch training. At the same time, I could never pick a Bb or an A out of thin air.
What I'm getting at is I think instrumentalists get pitch associations stuck in their head - when I imagine myself playing, and fingering Bb and A, I can sing the correct pitch. This in mind, how does this phenomenon fit in to learning perfect pitch? Should I think of my instrument and how it feels to play certain notes? Just basically, "what does it mean"? I've also had similar experiences in choral groups of singing a song over and over then days later I could find the starting pitch just by memory - "this song always sounds like this when it starts". - Adam
[I replied:]
Your description of your Bb-A fingering experience immediately reminds me of two anecdotal facts I've encountered.
One is that Beethoven continued to compose after he had become completely deaf-- and he still required a piano to do so. It seems that pressing the keys of the keyboard clearly evoked the musical tones in his head. He simply knew that when he pressed this key he'd hear that sound.
The other is the Suzuki violin teacher's description of her young students' experience. She says that when they begin learning their instrument, they associate the pitches that they hear with the position of their bodies. If she can teach them better physical balance (not always a steady thing at 3 years old), the physical sensation of each note becomes more consistent, and they become better at producing the musical pitches!
A third, admittedly, is my own experience-- until I wrote the computer program, it was much easier to remember the sound of a note if I pictured myself pressing the piano key.
You ask, "how does this phenomenon fit in" with learning perfect pitch, and my quick response is this: you can use it to your advantage.
It seems that an important reason why people do not develop absolute pitch-- even when they try-- is that they associate too much of the overall sensation with "pitch". This, I explained on my website at some length.. yet, up until you wrote to me, I knew that some people develop perfect pitch only on their own instrument, but I'd imagined that this was mainly because they included the overtone series of their particular instrument in their mental comprehension of "pitch". I had thought that the failure to identify notes on other instruments was principally due to the alteration of the overtone series; since the instrumentalist's sense of pitch was too broad, they as a listener would become confused when those overtones were changed or missing. But I had completely overlooked the possibility that a large component of their success in recognizing same-instrument notes could be because they remember the physical feeling of playing each particular note.
The single fact which has been clearest to me, from everything I've read, is that each pitch has its own unique sensory feeling, which is separate from any key signature or interval or "external reference". It's interesting to recognize that this is true both of the sound experience of pitches and of how you play the pitches-- that is, the unique feeling of a note is also accompanied by the unique feeling of how your fingers are positioned when you play Bb and A.
I understand that singers sometimes attempt to learn perfect pitch this way-- by trying to "feel" their throat when they sing certain pitches. There are dozens of reasons why this doesn't work: they may be sick on a certain day, or they sing when they've just woken up, or they're singing in a different style (jazz/pop/etc), and scores of other reasons pertaining to the flexibility of the vocal mechanism. But with an instrumentalist, the position of the fingers for certain pitches is immutable.
So how can you use this to your advantage? Get a partner to do the exercises
with. Whether that partner is another tuba player or a computer, what you need
to do is to condition the sensation of pitch away from your sensation of
fingering. Right now, what you're doing is evoking the pitch with your finger
movements. You want that to be the other way 'round. What I would expect to
produce the best results for you would be for someone to play you a tuba note,
and for you to say to yourself essentially this:
- "That note feels like [bright, soft, salty, whatever]."
- "Do I also feel that same way when I press these valves?"
- "Then that must be an A!"
By reversing your mental process in this way, you should begin to discriminate the finger motion as separate from the sensation of the pitch-- while at the same time you are using that familiar connection to your advantage, to reinforce your certainty of the unique feeling of each pitch. That is, you begin to understand (on a subconscious level) that your familiar pitch feeling is caused by, rather than part of, the feeling of finger movement.
I have learned that that's how people with absolute pitch play instruments-- they conceptualize the note they want to hear, and then they find the correct key/valve/fret to produce that note. That's why they find it so difficult to play an instrument that's out of tune-- not because the tunelessness causes them some kind of vague aesthetic distress, but because the notes they want aren't the notes they're getting and they become confused and frustrated. Additionally, that is, of course, why they often find it so easy to play multiple instruments. It's like a dancer learning different styles-- only the physical movements are different.
It also reminds me of pop songs on cassette tapes that I've listened to dozens of times-- sometimes I can't for the life of me remember a particular song from that tape, but as soon as I sing (or hear) the end of the song which immediately precedes it, I instantly remember it. Similarly, when I hear the ends of certain songs which I know from those tapes, I can't help but expect the first strains of the song which normally follows it on the cassette. I absolutely can't hear the closing strains of "I'm On My Way" by Captain & Tennille without expecting the lonely guitar that opens "Hope I Never Lose My Wallet" by the Mighty Mighty Bosstones-- and it's difficult to finish singing any song from Jesus Christ Superstar without launching right into the next one.
Interestingly, this tends not to work in the other direction; the opening of a song rarely makes me think of the previous one. Hm. I suspect that this might help explain why it's a good idea to let yourself reverse the note-sensation and finger-movement; if the end of one song and the beginning of another is a continuous mental event, then it's probably appropriate to think of the finger movement and the Bb as parallel, as a continuous mental event of sensory experience; by reversing the order, you are able to identify where the note sensation begins and the finger sensation ends.
[He then replied right back:]
I just want to clarify something... I used the word "phenomenon" specifically - that is, while I by no means would say I have perfect pitch, my little episode last night is characteristic of similar events that happen to me randomly. As in, hearing a song on the radio and without thinking walking over and slapping a key on the piano and it's the tonic. There's a feeling of just "knowing it's right" the moment before my finger hits the key-- in my experiences like this, "non thinking" seems to be a key element. It's almost as if perfect pitch is latent inside us all, it just somehow digging it out of our subconscious.
Just to make clear the reference to the tuba, on any brass instrument each valve combination can produce a variety of pitches depending on the firmness of your embouchure in the mouthpiece. The second valve that sounds A, also can sound E and C#. Its not necessarily the feeling of the valves, but combined with like I said its how I begin every warm up routine - the first thing I do every day, moving from my fundamental Bb down a half step. I think the "fundamentalness" of it is what makes it stick more so than say, D to C# which could be produced by the same valve combinations. Just wanted to clarify that...
At school today I kept thinking about how great musical life would be with perfect pitch. Sight singing class, dictation, my instrument, composition improvisation - it would all be so much improved. What a better chance I'd have at an awesome grad school! I'm going to get to work on this, thanks again for your help. Keep in touch.
I think he's absolutely right-- that it is the "fundamentalness" of the action which "makes it stick". Perfect pitch acquisition isn't the sort of understanding you can teach yourself actively and intellectually; you can only instill it with constant repetition and reinforcement. If you approach your perfect-pitch ear training this way, with the right exercises and an understanding of what you're doing, patience and persistence will win out.
From everything I can tell, he's completely right in his supposition-- that perfect pitch is something we all "possess" but have to dig out of our subconscious. We all hear the same things; we just have to respond to them differently. It's exciting to be doing the exercises and feel it coming; to listen to notes and simply know what pitch you're listening to. The experience is distinctly similar to what he describes.
I love it! Thanks for writing, guys.
I've already discovered that the vowel-association list which Peter presented me with appears to be relatively correct, but not absolutely so. I was therefore concerned that the vowels which I thought I heard in piano tones were things I was convincing myself I was hearing, especially since there was some dissent in the Yahoo discussion group about whether or not the same vowels were heard for each tone.
I recently discovered that Cool Edit Pro is capable of producing pure frequencies with overtones added, and I've been playing around with that using formant frequency and phonetic vowel guides.
While doing so, I took a page out of Mathieu's book. When I was listening to the two-frequency sounds which corresponded to the vowel associations, I sang the vowel I'd meant to create, at the apparent fundamental pitch of the sound. I was intrigued to notice that when I sang the vowel which mathematically corresponded to the tone I'd created, my voice combined with it, just as Mathieu suggested would happen for harmonic sounds; and when I sang a different vowel at the same pitch the feeling of connection fell away. This is encouraging, because it suggests a way that I can at least experientially (if not experimentally) support my idea that musical tones evoke specific vowels, even if vowels don't necessarily evoke specific musical tones.
In other news, earlier this week I was astonished and delighted to find that I was speaking with someone who had perfect pitch-- and lost it. I'll tell you more about her soon. It's most interesting.
Yesterday morning I drove to my rehearsal and I was trying to remember a choral part which is nothing more than a C repeated in rhythm. I had intended to play a C for myself, on the piano, before I left; but I'd forgotten to do so and I had at least half an hour before I had access to the rehearsal space. So in the car, I practiced what I thought was a C. Once I finally got to the rehearsal space, I strode directly to the piano, sung the note again, and plunk... I had it right.
Later on in the rehearsal, during a break, one of my castmates was trying to practice a different choral part and, away from the piano, couldn't quite decide on the correct opening pitch. I remembered that the opening pitch was a B; I stepped away for a moment, covered my ears, and recalled what I thought was a C; then I took that "down one" and sang it. Yes, that was definitely the first note of the choral part. I tapped him on the shoulder and gave him the B.
Between these two experiences, I'm most interested in the fact that I wasn't sure that I had it right-- even though I did. In the first instance, I needed the verification of the piano, and in the second, I wasn't certain until I matched the supposed B to the line of music which it began. This seems to support one of the premises of the effort-- that success is a matter of constant reinforcement until the connection between pitch and sensation becomes fully internalized. It also informs an idea that I've been very skeptical of-- that a person with perfect pitch has an "internal template" which matches notes to names. I had rejected the idea of a template because it seemed to be part of the geneticists' argument-- that there's some kind of hard-coded neural pattern in the brain which allows someone to identify notes. But it appears that literally it must be true; there must be some fully internalized reference which will allow a person to match their conscious sensation to their known experience. I don't have that template yet, but I'm intrigued that it seems to be coming into focus. I've ordered a book about memory which appears to be delayed by another three weeks. I'd be annoyed except for how much good material I still have yet to read.
When I'm doing perfect-pitch exercises, my "template" seems to be working decently well. I'm getting better at the exercises; enough so that I begin to understand how ridiculous it must be for someone who has perfect pitch to be "tested" by some researcher who's investigating the phenomenon. The color analogy is appropriate in this case; imagine some white-coated scientist showing you flash cards each with a different color. You would, of course, just look at each one and name them. There's no guesswork involved, and as the scientist marveled and exulted over your "achievement" you'd honestly wonder why this is supposed to be such a phenomenal thing. I can tell you that the analogy is on target because of how much easier it becomes for me to do an exercise if I simply say to myself, as I begin, "all I'm doing is telling myself which notes are playing." If I tell myself it's going to be hard, if I tell myself that I'm supposed to be "guessing", if I think that the goal is to figure it out, I don't do quite as well.
Today I was reading Why Smart People Make Big Money Mistakes, which is an entertaining and informative book. On page 144, I came across this example:
Imagine that sitting before you are four index cards. Each has a letter printed on one side and a number on the other. The sides facing up each show one of the following: A, B, 2, and 3. Your mission is to assess the validity of the following statement by turning over the fewest number of cards: "All cards with a vowel on one side have an even number on the other." Which cards would you turn over in order to determine if that statement is true or false?
(If you like simple puzzles and want to think about that for a moment, please do so before reading on.)
Now, this book is entirely about psychological fallacies; in every example up to this point the most obvious answer had been the incorrect one. So when I saw this problem, I instinctively chose "3" and then "A" as the ones to turn over, but wondered-- That's too easy. what trick are they about to pull? I was quite surprised to read that my "obvious" answer was actually the unusual one:
The confirmation bias... is hard to overcome because most people do not find it natural to do what is necessary to overcome it-- which is to deliberately seek answers that contradict their beliefs and preferences. This can be seen in the way people approach the card problem given here. Most people choose cards A and 2, or card A alone. ...The correct response would be to choose card A (to see if there's an even number on the other side) and card 3 (to make sure there's not a vowel there).
As you can imagine, the entire field of psychological pitch suffers from severe confirmation bias. If my correspondence with her and the interviews that I've read are any indication, Jane Gitschier won't seriously discuss research and ideas which don't contribute to knowing perfect pitch as genetically endowed. But most people who have opinions of perfect pitch are intensely entrenched in their opinions. I've mentioned before how I've used the Yahoo discussion group to test out some of the ideas I've developed on this website; but I've discovered there-- and elsewhere-- that mainly, the people who seem to be willing to consider new ideas are those who have not yet formed opinions (and people who haven't thought about it often surprise me by building meaningfully on the ideas I suggest to them). Once they've formed an opinion, however well or ill informed, they generally stick with it and won't be budged. Although I (seemingly) haven't swayed anyone in the Yahoo group to a new way of thinking, it's been enlightening to understand how each of the perspectives they insist on fit within the context of the evidence I've been assembling.
The universal stubbornness I've encountered has, of course, made me wonder if I was suffering from confirmation bias myself. I've found very little to contradict what I've concluded, and everything that I discover-- even tangentially-- seems to support rather than detract from what I've come to understand. I have had to wonder if somehow I wasn't finding only the answers I've been looking for. The example in this book at least assured me that I've got an appropriate instinct for seeking disconfirmation; and, as long as I don't allow myself to believe that I have the answers then I'll be open to new ideas even as I continue to bolster my theories.
So the other evening I was sitting with one of my castmates in the musical I'm currently performing, and of course the topic of perfect pitch eventually surfaced. "Oh, I've got that," she said. "Or at least-- I did." I was shocked; I didn't think it was possible to lose perfect pitch. It's something she had been able to do since she was very young, she said, and one day someone had told her that she had perfect pitch-- that sounded exactly like most stories I've heard. As I spoke with her about it further, she described how she managed to identify and reproduce notes. She said that when she heard a pitch, she'd test the pitch by feeling it within her throat where she'd sing it. She pointed at various places on her neck-- I feel A here, and C here, and so on. She said that for most of her life, she was able to identify and produce notes this way. But there had been a stretch of some time where she had been working outside of theater, and didn't sing or practice at all; and, when she returned to singing, she discovered that she had lost touch with the feelings that allowed her to demonstrate perfect pitch.
I was fascinated. It was clear from her descriptions that her claim to perfect pitch was legitimate, and that her possession of that skill had been strong and reliable right up until that period of (singing) inactivity. This also seemed in accordance with the message that another person had written me, to describe her experience of perfect pitch which she'd been "born with":
When I hear pitches, they resonate in different parts of my oral and nasal cavities. Isn't that weird? It's like I hear what it would be like to chew the notes. For example, G sort of twangs at my soft palate, like wasabi, while Ab is farther forward, right where my double-tongue point is (I'm a brass player).
What I thought I had on my hands, then, was a clear blow to the geneticist's argument-- if someone had been born with perfect pitch, if they had a genetic coding which had definitely been "activated", then surely it wouldn't be possible to lose it! If the genetics researchers are right, then a child "learns" perfect pitch through exposure to musical training, which somehow activates their perfect-pitch gene-- but what if the child makes the wrong association with their pitch perception? I'm eager for definitive proof against the genetics-only argument, especially the genetics-learning theory (which, according to my research, is unsupportable), and this seemed to be it.
As I thought about it, though, over the next few days, I became a bit uneasy about making any sort of broad statement-- I didn't know that this woman had been born with perfect pitch. I knew little more than what I've just written here. At last night's rehearsal, then, I took advantage of a break to ask her if she'd always had perfect pitch; and, unfortunately, the answer was no. She said that she had not always heard the pitches distinctly, but that during her vocal training she had learned to make the associations between the pitch experience and her throat's sensation.
After a moment of disappointment, being frustrated that this wasn't the proof I had been looking for, I began to consider instead what was implied by her statements.
She spontaneously developed perfect pitch. If the genetics folks are right, then her development of perfect pitch could be explained by the activation of some gene through early musical training. But what if it simply happened because she figured it out for herself? This would utterly validate the notion that perfect pitch can be learned, and this seems possible because
She lost her ability of perfect pitch. This loss occurred as an adult, and she was able to coherently describe this experience as one of deteriorated psychological association and memory. If pitch had somehow been genetically coded into her brain, how could it have been lost? (If you happen to have an explanation of how it could, please tell me.)
She had a physical association for every note. The tuba player I've quoted mentions how he has a distinct physical association for certain "fundamental" pitches; given this woman's experience (and the fact that a deaf Beethoven composed by using a piano) it seems appropriate to imagine that developing perfect pitch on one's own instrument is not only possible, but probable, if the musician is adequately proficient. In this case, of course, her instrument is her voice (she has her MFA from Juilliard). It makes me wonder if people who have demonstrated instrument-specific perfect pitch will all tell you that they include physical memory in their comprehension of pitch, or if to them it is purely listening.
This also sheds some light on the veracity of what I've been saying all along about learning perfect pitch by how it feels in your throat. Although it is possible to do so, and although it is an effective technique, it is no more or less effective than memorizing how it feels to press the keys of a piano, pluck a guitar, or bow a viola. By the very nature of the association, as a listening skill it is incomplete, "slow", unreliable, and ultimately insecure.
I'm sure there's more to be gleaned from this particular case, but for now I'm satisfied.