
Acoustic Learning,
Inc.
Absolute Pitch research, ear training and more
Last night, at the grocery store, I bumped into my voice teacher. We exchanged a surprised greeting and, each wondering what the other was up to, spent the next hour standing in front of the pickles and mustard excitedly discussing singing, hearing, and pitch. She told me how she's aggressively pursuing her new theories about laryngeal "lean" (you'll have to ask her-- it's fascinating stuff); I mentioned how I was trying to discover a bridge between absolute and relative listening. As I described to her my recent topics of harmony and implicit motion, I learned I had been making a very wrong assumption.
When I said to her, "If you've got highly-developed relative pitch, which you have, and you instantly identify an interval by its single harmonic sensation, that's like perfect pitch," she looked at me curiously and said "But that doesn't happen." To my great surprise, she informed me that her relative-pitch skill, which is top-notch, means that she has effective intellectual strategies to recognize most intervals-- such as comparing a major sixth to the opening notes of "My Bonnie". Does this mean, I asked incredulously, that you don't hear the intervals' harmonic sensation at all? Well, she replied, for the smaller intervals I do hear the unique characteristics, but after a perfect fifth it's not instantaneous or automatic. With intervals wider than a perfect fifth, she said, it has to be figured out.
You can see by analogy how wider intervals, as an implicit distance, would be more difficult to recognize. Imagine trying to judge a physical distance by sight. You can precisely recognize 2 or 3 inches without help, but if something could be either 74 or 75 inches you have to measure it to be sure. Once I'd left the grocery store, I related this part of the conversation to Gina, who holds her MFA in musical theater-- she laughed that yes, of course it's like that after a perfect fifth. The wider the notes, the harder it is to figure, she shrugged; and she said it as though it were common knowledge.
I was astonished to discover that a person with advanced relative pitch would not have been trained to listen harmonically. It was remarkable to learn that lack of harmonic perception is considered normal. It was even more perplexing to realize that, after decades of training and teaching and musical experience, it would not even have occurred to someone to try listening harmonically. In traditional musical comprehension, an interval is the distance between the notes, and that's all there is to it.
But distance shouldn't matter, I thought. If the interval is defined as the harmonic ratio, then a harmonic listener would instantly recognize an interval as a single sensation regardless of the "distance" between the notes. Yet I'd been wrong to expect that a relative listener hears intervals harmonically. Might I be wrong that an absolute listener hears them harmonically? Miyazaki's research on "perfect pitch as an inability" showed how some people with absolute pitch attempted to identify intervals by counting scale steps (although as letter names, not as "distance")-- perhaps someone with perfect pitch, who has learned to identify intervals, is not identifying them harmonically? Perhaps they're using some other strategy!
Wanting to be sure, I fired off a message to IronMan Curtis as soon as possible. He has excellent perfect pitch, and he can easily identify intervals, although he has often said that he has absolutely no understanding of what it means to hear in relative pitch. I wanted to ask him about wide intervals. "Do you recognize a major seventh," I asked him, "because of the 'distance' between the notes? Or do you know it because it 'sounds like a seventh', or perhaps because when you hear the two notes you can calculate the seven scale steps between them? Or is it something else entirely?" Fortunately, he was very quick to reply, and I was relieved to know I hadn't been mistaken.
Good question. I hear the notes, of course. I also hear the harmony. I recognize both as a M7 intellectually. The distance doesn't much matter unless it's huge or in the bass register where close intervals become muddied. It can be a semitone (as when an M7 chord is played with one "normal size" hand on piano), nearly an octave, several octaves, etc.
Harmonic listening exists; and, if it's not normally taught (or even considered), I'm even more encouraged that it may be a connection between relative and perfect pitch. Mathieu shows, mathematically, how harmonic ratios and scalar distances are one and the same thing. But if it's possible to determine a scalar distance with no sense of the harmonic ratio, and it is also possible to identify an interval with complete disregard for scalar distance, then harmony and distance must be two completely separate psychological processes-- two aspects of the same experience, just like Mathieu said. All listeners hear the same harmonic ratio, but most people listen for distance. Relative listeners do not know how to listen for the harmony!
But wait a minute-- for intervals smaller than a perfect fifth, relative listeners do hear the harmony. Why would they hear it at all, if they don't know how to listen for harmony? If they hear harmony for smaller intervals, why don't they hear it for wider intervals? And why is the perfect fifth generally recognized as where it starts to get difficult?
For answers to these questions and more... stay tuned!
There's been remarkable response to the previous entry. I had intended to use this next entry to offer my answers to the questions I'd posed, but considering the number of people who wrote me to say that they were "amazed", "astonished", or "compelled to write", and who really took the time to thoughtfully explore with me how they sense and perceive music, there are some thoughts which must be shared first. It seems fair to say that there's something very intriguing about harmonic listening versus distance judgment. Phil said it most clearly: "...I'm not sure that people even THINK along the lines that you are thinking," and that's the crux of it.
In the responses that I've received, it appears that most people never considered whether they're listening harmonically or by distance judgment. As far as anyone knew, what they've perceived is simply the way sound is heard, so there's no reason to even consider a critical examination of that perception-- any more than you'd wonder if there's anyone in the world who can't see through a glass window. It just works that way. Accordingly, it's never occurred to most people that others would hear intervals any differently, and it's been remarkable for everyone to recognize that it ain't necessarily so. Each person that wrote me explained how they hear an interval, and it seemed from their writing that this was the first time they had tried to explain it, even to themselves. Clint, who maintains the Prolobe site for perfect pitch training, was one of the first to offer his insight.
I was reading your most recent entry, and you have me totally dumbfounded. I think this is because I do hear in harmony and your statements about people not hearing harmonies after a 5th are strangely unknown to me. I don’t recognize intervals by some computation of the intellect. At least I don’t think I do. If you play any two notes together or one right after another, they create a sensation of distance like you describe. You can hear the pitch of each granted, but if they are close enough (in time not distance) together, a third "thing" is perceived, Using this "thing" to identify an interval is the easiest way to do it, no matter how far the notes are apart (at least for me). Now, I see where the confusion is when the interval is say more than 2 or 3 octaves, but that’s because I don’t even know what they are called. If you play a compound 7th or 9th pretty much anywhere, I hear it very similarly. The best way I can describe it is the 7th always has that tense feel to it and a 9th always reminds me of a jazz feel. ...It’s almost like you are describing that people need a reference to base their reference on. Hahaha, absolute relative pitch: the ability to listen harmonically without a point of reference.
Naturally, his comment begs the question, what is this third thing? Literally, it seems evident that the "thing" is Clint's perception of the harmonic ratio of the two notes. But is this "thing", which Clint perceives as a harmonic interaction, actually the same thing which would another listener would judge as distance? Are there only three things, and the third thing is interpreted either as harmony or distance-- but not both? Or is distance a different sensation altogether, a fourth "thing" created by the two notes, which exists in addition to the harmony? According to Rich's experience, there is definitely a "fourth thing", and that fourth thing is distance. Your mind can simultaneously, and separately, perceive both harmony and distance.
[Harmonic listening] may explain a difficulty I always had prior to doing any ear training. When transcribing (or even just singing along with the radio) I would often be confused by a melodic step that would be ascending but depressing (or descending and uplifting) at the same time. I now understand that this happened when a melody would ascend scalar steps, but land on a more harmonically complex note (or the opposite). A P5 to a m6 would be a close interval example. Prior to any ear training, I would be confused by such an interval. My head would be telling me "up," but my gut would be telling me "down." Wider intervals would simply be confusing as hell. Obviously, the direction would be up, but I'd have no idea by how much. Now that I've progressed with the [harmonic ear-training] method, bolstered by the understanding of harmonic ratios, these steps are much easier. I'm not thinking "a minor second up," I'm thinking "sol to le." It's still relative listening, but the listening part is based on harmony with the common root, which can quickly be translated to scalar steps so my brain can tell my fingers to move up one fret. This has had the ancillary benefit of really opening up the fretboard to me, so I'm improving greatly as a guitar player. I, like many rock guitarists, was really a slave to the "boxes" (fretboard patterns for scales and modes.) Now for me, the boxes are gone, and the entire fretboard is one big land of chromatic possibility. ...The distance between notes doesn't matter as much since you've memorized the sound of each scalar note. In fact, even large octave distances do not confuse the ear. A "ti" in any octave is still clearly a "ti." It is true that the extreme upper and lower registers are a bit difficult to distinguish, but identification of any single note in any register is quite easy once you've got a sense of key.
The traditional musical scale is a convenient construct that is the result of, not the beginning of, musical harmony and melodic perception. Mathieu, in Harmonic Experience, demonstrates how scales are actually constructed from harmonic relationships. I'll have to illustrate this point later on, with Mathieu's step-by-step demonstration (and probably with the psychological principles described in Thinking In Sound), but it's more than I can explain now. Right now, I ask you to accept this assertion at face value, because that way I can point out how Rich's musicianship begins in harmony, and is translated to scale steps. Phil has had a similar experience:
That is how I navigate while improvising. ...You mentioned that "the wider the notes, the harder it is to figure..." I don't have that problem at all, because I identify notes via harmonic sensing or scale degrees. ...Any note in the scale, no matter how distant, even in an octave 3 or 4 octaves away, is immediately obvious to me-- as long as the key does not change. But when the key changes, I have to discern in which key my unconscious RP is hearing, and as soon as I discover the key... then I can reset my scale degrees to the new key. ...I came to the conclusion that "I do NOT think in intervals". ...I realized that I stink in naming intervals. Yes, of course I could do it, but not nearly as well as I could find notes on the keyboard. So I said to myself, "Well, what the heck ARE you doing then?" and I realized that I was hearing and identifying notes as scale degrees.
Scale degrees are not the same thing as scalar steps! Mathieu's demonstration shows not only that the traditional scale is constructed from harmonic relationships, but that it is constructed out of order. Considering the seven steps of a C-major scale (excluding the accidentals), Mathieu says, with typical good humor (but with my emphasis),
While you are singing, remember to appreciate that, in harmonic terms, C and D are not neighbors but live two houses away. One might ask the riddle, "Harmonically speaking, what lies between C and D?" (If you say "C#" or "Db" the author will have to immolate himself immediately.) Awareness of the reality in which G lives between C and D-- whether or not it is being heard as a note in the air-- is the goal.
I highlight that last sentence because, potentially, this is as critically important as the realization that the goal of perfect-pitch training is not "naming notes". The goal of relative pitch training is not "naming intervals". In this view, relative-pitch training should emphasize harmonic recognition. David presents a compelling case for this.
I don't know why people persist with interval-based relative pitch methods. I've wasted my fair share of time on them and it has never done anything to help me play music. It doesn't seem of much practical use, especially to the improvising musician. So I'm in a band situation and I hear a major 6th ("My Bonnie")-- just knowing this tells me nothing useful in an improvising situation-- it could be any of a number of major 6th's in the current improvising key. I need context. I need to hear the pitches harmonically in the key of the improvisation to know anything useful. If you can get this type of listening down, to the point that you just know a note is a maj7 or min3 (or whatever) within the current key (ie. no "My Bonnie" or any other interval based tricks like singing up/down a scale) and you can retain permanent memory of just one key absolutely (say, for example, C major). Then you could technically claim to have perfect pitch. To identify notes you start hearing your key of C major in your head and a note comes along and it's a maj6 harmonically then you know it's an A. This method would be instantaneous. I remember reading somewhere that if someone's comparing a note to a reference then some people consider this not to be "real" perfect pitch. But I think there's an assumption in the statement that the person it singing up/down intervals and so the recognition won't be instantaneous. In the method I'm suggesting there's no such comparison, there's just listening in a C major context to a note. Also, someone might argue that it's not perfect pitch because you're identifying a maj6 rather than the note A. But this is just a labeling issue. So you call it "A", well my name for it is "maj6". I can easily just learn the note names rather than interval names and internalize this to the point where I'm labeling notes by name instantaneously. Maybe everyone who have perfect pitch uses this technique but do it intuitively. Each person could have a fundamental key that they hear naturally. Different may be in different keys but the method would remain the same. I definitely think you're on the right track with harmonic listening. I think this is the path to better musical perception. Forget about interval based relative pitch.
I agree almost completely with David's observations. Miyazaki's research shows that people with perfect pitch become unable to name notes (played in intervals) when their tonal center is shifted-- as David speculates, this suggests that people with absolute pitch may identify notes by their harmonic scale degree, and that having relative pitch isn't necessarily a barrier to, or even any different from, having perfect pitch. This is similar to what I was previously describing from my own experience, hearing the major third of Free to Be You and Me. Because my mind knew that the sound was a major third, starting on an Eb, I simply knew that there was another note that was a G. The Eb was a reference point, sort of, but David has quite concisely illustrated how this is different from typical distance judgment.
Some of the people I've quoted here have tried and are using the Bruce Arnold relative-pitch method. I originally recommended the Arnold method because his "one note method" seemed very similar to perfect pitch training, even though at the time I hadn't really understood the principle of harmonic listening. Now I know that Bruce Arnold's method is that of harmonic listening, and Rich says that Arnold completely disavows any value in intervallic distance.
I have the "Complete One-Note Method," and emailed a question to [Arnold] about accelerating progress and if traditional interval ear training could be used to supplement his method. His response emphatically discouraged using traditional interval training as incompatible and unproductive; however, he did not offer any rationale for his advice and recommended that I should buy [Arnold's book] "Fanatic's Guide to Ear Training and Sight Singing." Arnold repeatedly lambastes traditional interval ear training methods as too limiting.
Admittedly, it is tempting, especially from the evidence you've just read, to agree with David, Phil, and Bruce Arnold, and conclude that distance training is completely useless. But is interval identification useless? Would it be better just to learn to hear harmonically, and forget about intervals altogether? I might have been convinced-- but I've recently heard from Kevin, a new voice which gives me pause. He began by describing his experience of musical listening, which I found fascinating.
I started out learning to read music and did no playing by ear. Later on I took three semesters of music theory at a local college. I aced the written part and flunked the ear training. I sang in choir by trying to hear a strong voice singing my part and frequently got lost. Music school and I parted ways when I found they were teaching me theory but had absolutely no idea how to teach music comprehension... It was as if a blind man was trying to understand how a rainbow looks to a sighted person. They understood it but could not impart that light bulb to me.
You asked me to describe how I hear sound. Have you ever seen sound on an oscilloscope? The violin is a big fuzzy batch of vibrations. Not a clean sine wave at all. That is the best visual way I have of describing it. My mind hears all this vibration, different beats, consonance, and dissonance happening all at once. The more I concentrate the more I hear dissonance in all intervals and soon cannot identify a major 3rd from a perfect 5th. One instructor was testing me and noticed that I heard intervals differently when played from a different starting note. Start on a C and play a perfect 4th on the piano and I could identify it. Play that same interval, starting on an F#, and I would become confused because it was a different sound. I have started playing the violin by ear. I tune the G, A, & D strings with not much problem. But the wire E string sounds so different from the wrapped A string that I have problems identifying the off key beats. I hear many levels of things going on in that fifth. One series of beats in the E/A sound depends on how fast I move the bow.
Kevin has neither relative nor perfect pitch-- but he hears harmonically. Or at least, so it seemed. How could I find out for sure? I reasoned that if he heard harmonically, he would not hear implicit motion and note acceleration. I wrote him again, and I was thrilled by his reply:
To answer your question I don't notice an emotional lift going up the scale or an emotional drop the other way. What I do notice when playing scales is a relief when hitting the tonic. It is like a big landing pad or target to me. I tend to want to stay there and relax. Come to think of it what I notice playing scales is when going both ways a sense of tension until I hit the tonic.
(From my research, I believe that what he is describing is a sensitivity to harmonic ratios, which "comes to rest" when reaching the 1:1 constancy of the tonic. This "tension" may prove to be the bridge with which to explain relative listening to the absolute hearer, but I will have to pick up that topic later.)
There must be a connection between scale degrees and scale steps; otherwise, how could Phil know where to find the right key on the keyboard? Rich may not be thinking "minor second up", but he still perceives a one instead of a nine. Even if only for the fact that you have to sit down and play with instruments that are designed for the traditional musical scale, there must be some perception of distance, or your musical proficiency will suffer. The only question is...
...why?
Although the perfect fifth may be a threshold for most people, it's not an insurmountable obstacle. Using my analogy from before, of judging visual distances, it's possible to imagine that a skilled carpenter could precisely recognize a piece of wood to be 72 or 73 inches, without having to measure. He just has to work with those distances frequently enough to become intimately familiar with them. Paul confirmed that, in his personal experience, he can accurately judge wider distances irrespective of their harmonic sensation.
One learns to "feel" it after intellectualizing-- it comes intuitively. I'm assuming this is the same with Absolute hearing. (I find myself sometimes having to figure out what a 3rd is just as much a 9th or 10th.)
When I protested that distance judging is not "compatible" with musical harmony, Paul remarked quite pointedly:
Yes, perhaps. But as you state in your research, absolute hearing has nothing to do with music. This is an important statement because anyone who cares to develop absolute hearing has intellectualized the process of relative hearing and all aural perception is conditioned by this.
It seems probable to me that distance learning is to interval perception what vowel sounds are to pitch perception. It's an intellectual process, not an emotional one, and it allows us to create a literal recognition of an intangible experience-- but just as a pitch is not a vowel, an interval is not a distance. Vowels and distances are shortcuts to intellectual comprehension; they are not the true sensory perception. But both perspectives are necessary. A harmonic listener, lacking distance judgment, is confused when the context changes; a normal relative listener, who has no harmonic perception, is confused when the distance widens. Distance judgment, harmonic listening, vowel sounds, trigger words-- for total ear training, all methods must be employed.
I have a Nintendo 64 emulator on my computer, and the only game I have for it is "Banjo-Kazooie". I've had-- and finished-- both "Super Mario 64" and "Paper Mario", but for some reason I keep coming back to Banjo-Kazooie (which is odd, because usually I don't have much patience for games after I've finished them). I think I've played it from beginning to end about a half a dozen times; I try to see how much more quickly I can blaze through the worlds, and each puzzle is consistently entertaining-- with one exception.
Each time through, I've found one particular objective rather tedious. It's a classic memory game; there are six turtles, and they each make a little "yarp" sound, and you're supposed to remember the random order in which they speak. You can see, in the picture below, the turtle on the right making the noise.

Each time I've reached this point in the game it's been frustratingly difficult. First they ask you to remember three random turtles, then five, then seven. The memory part wouldn't be difficult-- the human mind is perfectly capable of holding seven bits of information in short-term memory. What had always irritated me about this section is that, after the turtles had finished, the game always flipped to this different perspective:

It was impossible to prevent the screen from changing camera angles, and it made the game so much more difficult! "Back left" was now "upper right"; "very front" was now "middle left"; and even the one which (in the first perspective) was very clearly "center" was now more "middle right" to my eyes. I was still able to manage three turtles easily, and five with some difficulty-- but every time it got to seven, I had to make a diagram, mark down the order, and then physically turn the diagram in front of me so I could recognize which turtle was which.
Last night, I again made it to this spot, and sighed as I prepared for the same frustration-- but I suddenly noticed something I hadn't before, which made me feel quite stupid. The turtles were all different colors. Needless to say, once I saw this, I had no problem at all... and once I'd finished, I realized that I hadn't even thought about where each turtle was standing.
My original strategy for solving the turtle problem is very similar to someone with perfect pitch trying to recognize a transposed melody. Miyazaki did an experiment in which he asked people with perfect pitch to identify transposed melodies. He either showed the listeners a musical score, or played them a short melody, and then played a similar comparison melody which sometimes had a note altered. They were asked, were the two melodies the same or different? People with perfect pitch did rather poorly at this task, and the most revealing part of the experiment is the method by which the absolute listeners typically attempted to solve the problem.

The absolute respondents described how, when trying to compare the melodies, they didn't just try to hear the relationships of the notes to each other. They attempted to visualize the new melody on the musical staff, so that they could decide if it "looked" the same as the other one. When I wrote down the positions of the turtles and rotated the paper, I was doing the same thing-- trying to identify the absolute positions of the turtles, even though I didn't have the correct colors to work with.
The turtle example shows how harmonic listening from a tonic could be helpful. I had tried to identify each turtle by its absolute position-- "front right" or "rear left" in relation to a fixed perspective. But I probably would have had more success if I had named the turtles "front right" or "rear left" in relation to the center turtle. The center turtle would have been my "tonic", to which I related all the other turtles. Then I would not have been confused no matter which way the screen was turned, and I would have been able to do this without using the colors on the turtles' backs.
The main reason I mention this analogy, though, is to wonder if it indirectly illustrates a need for distance perception. There are only six turtles in this picture, and therefore (with the center turtle as the "tonic") there's only one turtle which can be described harmonically as "left front". But what if there were another turtle which was also to the left and in front? How would you tell them apart? You'd have to say "...and two inches further" in order to know which one you were talking about. Can this distance be accounted for solely by harmonic perception? If the harmonic listener is indifferent to distance, and hears "mi" as "mi" regardless of the octave, then what's the perceptual difference between 3:1 and 3:2 which helps tell them apart? After all, harmonic relative pitch tells you a relative position— it's distance relative pitch that gives you an absolute position! (That seems like a contradiction!)
I'll have to keep this in mind because I don't have a definite answer right now. In any case, these turtles have helped to remind me that musical constructs are also spatial-relationship problems.
In order to address the questions I posed a couple entries ago, I need to explain Mathieu's harmonic scale. It's not actually a "scale" but a lattice, from which a relative scale can be constructed. Its origin, and the thesis of Mathieu's book, is stated and restated at the beginning of his seventh and eighth chapters (p 42, 47):
Our operational premise is this: Harmony consists of perfect fifths, major thirds, their compounds, and their reciprocals... Rephrasing, [t]here are two harmonic elements, fifths and thirds, subject to two procedures, above and below.
In his exercise which I presented here on June 3, you were able to hear how a major seventh is a harmonic compound, combining of the ratios of a fifth (3:2) and third (5:4), the first two non-octave partials. Mathieu contends, as the heart of his book, that all harmonic intervals are compounds of these two ratios. Once you begin at the tonic, when you "add one" you don't create a minor second. You create a perfect fifth-- or a major third.

Mathieu uses multiple staves with identical clefs in order to keep the thirds
and fifths visually separate.
In the harmonic structure there are two choices for "adding one"! That's because the nature of this lattice is not to go up in distance like the relative scale, but to expand outward into harmonic complexity. As Mathieu describes it, "[music] is made... from the center out, more like the concentric forces of an atom, or-- to fairly include gravity into the metaphor-- like the limbs and roots of a tree." (p 59). You move along a lattice of fifths and thirds; the further out you go, the more harmonically "distant" you are from the tonic. It's somewhat confusing that Mathieu uses the normal relative scale to represent this lattice, because the notes in the normal scale appear "out of order" as a result.
For example: on the normal scale, if you start at the C and "add two notes", you must use D and then E:

But if you start at the C, and "add two notes" of the harmonic lattice, you could add G, then D. This happens just by compounding two perfect fifths.


If you wanted to add E and B, you could do so by compounding major thirds to both the C and the G; you've now created a five-note scale.

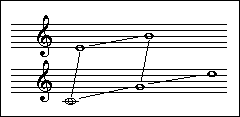
Just a few more additions and you have all seven tones of the C-major scale.


If you continue this harmonic mapping, you end up with all twelve tones of the chromatic scale.

As you can see, the "up" and "down" of the traditional musical scale seems pretty meaningless when you look at it this way. But Mathieu's diagram, and his metaphor, still maintain "up" and "down" orientations-- because Mathieu contends that ups, downs, and "distance" on the harmonic lattice translate directly to emotional response. Major notes are "up" from the tonic, minor notes are "down", and the eerie augmented fourth is one of the most harmonically distant notes. You can build a minor scale just by going down instead of up in the harmonic lattice. Mathieu names specific emotional metaphors for each type of movement along the paths; he doesn't insist on them, because no two people are precisely alike, but I find that they are interesting suggestions to give you an idea of what to expect.
Dissect the lattice however you wish. Play the notes on your instrument, move around the bars of the lattice, and hear how they relate to each other harmonically (try C-G-D-F#, perhaps). Try to hear the compounding; be aware of when you hear minor, when you hear major, when you hear consonance, when you hear dissonance, and imagine yourself on this map.
I started looking into the question of why the perfect fifth is a natural limit for distance judgment. The answer that I discovered surprised me, because it revealed that the fifth really isn't a "limit" beyond which our distance faculties are incapable of judging well. Rather, there are specific reasons why we hear the first seven intervals of the scale (m2, M2, m3, M3, p4, a4, p5), and those reasons aren't distance. The reason is harmony-- and biology. (For Phil's sake, I'll remind you that when I talk about hearing an interval "harmonically" I mean "as a single sound sensation", as opposed to two notes with a distance between them.)
My voice teacher told me that, even though she had been trained to hear intervals as distances, she nonetheless heard small intervals harmonically, up to a major third. I thought perhaps this was a psychological effect-- since the brain interprets similar pitches to be from the same sound source-- but the answer turned out to be biological. That is, it's impossible not to hear any of the first four intervals as a harmonic sound, because of the way the ear is constructed. If you go all the way back and remember how the basilar membrane works, you'll recall that even though every pitch has a specific place at which it peaks on the basilar membrane, the area around that peak is warped by virtue of the membrane being continuous. When pitches that are near each other sound simultaneously, the area of each overlaps. The nearer the pitches, the greater the overlap, until the pitches are indistinguishable as separate sounds.
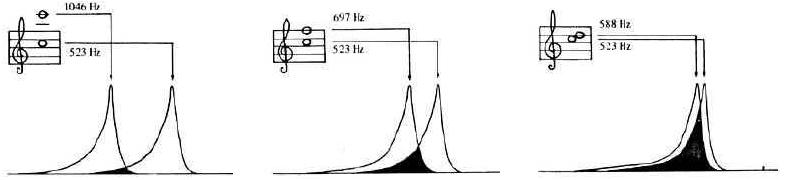
The distance at which the pitches cease to be distinct sounds and fuse into a single sensation is called the critical bandwidth. Across the entire basilar membrane, the average width of the critical band is one-third of an octave... a major third. We automatically hear that interval, and anything smaller, as a single harmonic sound.
It may be obvious from Mathieu's explanation of how to construct the relative scale, but I should point out that harmony comes first. When we hear an interval, the first thing that we hear is the notes' harmonic relationship to each other. The distance we infer comes afterward, as an intellectual interpretation of the sound. That is, when a person listens to intervals by judging their distance, they are sensing the harmonic information, but failing to interpret it. I'll go back to Rich's explanation of this perspective:
I now understand that [confusion] happened when a melody would ascend scalar steps, but land on a more harmonically complex note (or the opposite). A P5 to a m6 would be a close interval example. Prior to any ear training, I would be confused by such an interval. My head would be telling me "up," but my gut would be telling me "down."
This helps explain why there is, consistently, a sudden divide between the perfect fifth and minor sixth. It's not because of the scalar distance. If you think of intervals as "distance", common sense would seem to suggest that a minor sixth shouldn't be any more difficult to identify than a perfect fifth. After all, they're only one half-step apart. But harmonically, a minor sixth isn't "one half step up" from a perfect fifth. On Mathieu's lattice, the minor sixth is not only two harmonic steps away from the perfect fifth, but it has a qualitatively different relationship to the tonic-- down instead of up.

If you listen to either of these two intervals, expecting them to be very similar to each other, that expectation could make it very confusing-- because harmonically they're quite different.
But the reason we recognize the perfect fifth so easily is not because we are able to judge its distance. Aside from the octave, the perfect fifth is the most consonant interval that exists. With its 3:2 harmonic ratio, its familiarity stems from its sheer simplicity-- and, according to Mathieu, the perfect fifth is the most basic building block of all musical harmony. We hear the perfect fifth for what it is because, of all the intervals, this is the one which we would hear harmonically. This has been verified by people looking into the principle of tonal fusion:
Carl Stumpf carried out a seminal experiment investigating the tendency for some sound combinations to cohere into a single sound image through a process of Tonverschmelzung or tonal fusion. Listeners heard two concurrent tones and were asked to judge whether they heard a single tone or two tones. Stumpf found that the pitch interval that most encourages tonal fusion is the aptly named unison. The second most fused interval is the octave, whereas the third most fused interval is the perfect fifth (Stumpf, 1890). (There is no general agreement in the literature concerning the rank order for subsequent intervals. Some commentators consider the perfect fourth (3:4) to be the next most fused interval, whereas others have suggested the double octave (1:4). Experimental data collected by DeWitt and Crowder (pp.77-78) paradoxically suggests that major sevenths are more prone to tonal fusion than perfect fourths.)
A glance at Mathieu's lattice offers an explanation of why this would be so. The perfect fifth is the most consonant, and the perfect fourth is the reciprocal of the fifth.
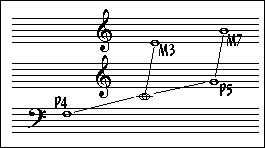
Although it is surprising that the major seventh would be more commonly fused than the perfect fourth, it doesn't seem to be a "paradox". I suspect that this is because the seventh is the simplest compound that can be created, as the combination of one perfect fifth and one major third. It may be easier for our mind to "add" intervals together than to "subtract" them-- which would also explain why the third's reciprocal (the minor sixth) does not appear as one of these tonal fusions. "Going down" in this lattice means adding harmonic complexity. Still, you'd think that the major third would be even more likely to be fused, not only because of its harmonic relationship but because of the critical band; I wonder why it's not mentioned. Fortunately, for our purposes, it doesn't really matter.
We now have specific answers for why we can identify small intervals, and it's not "distance". Up to a major third, the critical band forces us to hear the sound harmonically. The perfect fourth and fifth are products of natural tonal fusion. This leaves only the augmented fourth-- which happens to be the most dissonant interval of the entire scale. It's possible that the two fourths, perfect and augmented, are recognized harmonically because of tonal fusion and total dissonance; but it's also true that they're not always recognized anyway. My voice teacher said that sometimes she has to identify a fourth by comparing to see if a major third can "fit inside of it." Even though the fourths' intervals are smaller than the fifth, they are still more difficult to recognize than the fifth-- but, since the fourths can be heard harmonically, the perfect fifth seems to be a limit.
If you think that intervals are defined by their distance, it really truly appears as though your distance judgment fails after the perfect fifth. You can recognize the smaller intervals (up to M3) automatically; sometimes you have a little trouble with the fourths, but you nail the fifth every time before losing it at the minor sixth. It certainly seems as though the intervals get "wider" until you can't tell any more. But it isn't your distance judgment which allows you to hear these smaller intervals automatically. It's your harmonic sense (whether or not that sense is helped along by the critical band). In every case, regardless of the interval's "width", you apply your distance judgment as an intellectual calculation, after you hear-- and typically ignore-- the harmonic sound.
Once you've discovered what it means to hear harmonically, it's tempting to dismiss distance as useless. You might call it a nonexistent illusion, or the perceptual choice of the unenlightened. Bruce Arnold goes so far as to actively discourage distance education as harmful. But the fact is that harmony creates distance, and that distance must be reckoned with-- if even for no better reason than the fact that it exists.
I wanted to be sure that harmonic ratios and scale steps were the same thing in equal temperament. I found an encyclopedic listing of harmonic ratios, and I made an Excel spreadsheet to test them out. After all, the simple compounding of 3/2 * 5/4 = 15/8 works in just intonation, but the ratios in equal temperament are more complex. How complex? Complex enough that I should reassure you I'm not actually going to try to lead you into mathematical stuff here. All I wanted to know was whether the complex equal-temperament ratios also multiplied to make scale degrees. So when you see these equal-tempered ratios, you don't have to run screaming. I-- or, more accurately, Excel-- already did the work.
|
minor second |
196/185 |
| major second | 55/49 |
| minor third | 44/37 |
| major third | 635/504 |
| perfect fourth | 295/221 |
| augmented fourth | 1393/985 |
| perfect fifth | 442/295 |
| minor sixth | 1008/635 |
| major sixth | 37/22 |
| minor seventh | 1527/857 |
| major seventh | 185/98 |
Yecch! It's no wonder that Just Intonation has its adherents. These numbers are just ugly. The raw numbers are very similar to just intonation, of course-- the perfect fifth is merely 1.498 instead of 1.5-- but as fractions, the ratios are icky. Nonetheless, they still add up precisely as they should. On the Excel sheet I "added" the various intervals together by multiplying their ratios, and sure enough, they came out just right. Pick any intervals and compound 'em. Minor sixth + major third = octave, and major second + major third = augmented fourth, regardless of what system you're using.
Mathematically, it's true that distance is harmony. If you have to choose one style over the other, it seems obvious that harmonic listening is the only way to go. But, psychologically, distance is not harmony. They're not exclusive interpretations; they're two entirely different experiences of the same physical input. Before we can ask which one is better-- or even if one is better-- we have to figure out how to compare the two.
I looked for someone who had already attempted to make the comparison, but according to Google, only one page on the entire web even acknowledges any difference between scalar and harmonic listening. Fortunately, that page from Sonic Arts made its point concisely. "Harmonic listening is bound to force one to think in terms of ratios, while scalar listening encourages thinking in terms of 'steps' (unequal or equal)." How you listen to music determines what you get from it, and this perspective makes it possible to frame the question objectively: When is it more valuable to think in terms of ratios, and when is it more valuable to think in terms of steps? If Bruce Arnold is telling you that steps are unimportant, then that would imply it's never valuable to think in terms of steps; that seems unlikely to me.
I wanted to hear from someone who could speculate on the value of scalar steps. After reading one of Mel Martin's on-line columns, which describes the essential role of harmonic perception in jazz performance, I asked him what he thought of the issue. He replied:
My whole experience with music is about expression of emotion. Harmonic hearing, or the ability to know the sound of chords, is essential to doing that, since harmony expresses mood and feeling while melody is the singular focus for the listener.
By coincidence, Alain wrote me shortly after with a related opinion.
...[Y]ou should know both equally well. Why? Because when you transcribe music and you write down a melody or solo note for note, when you write down the next note you can use one of the two methods: hear what the function is of that note in the context of the key OR identify the interval it forms with the previous note. Then... you verify the note you just wrote down with the other method so you're certain the note you wrote down is correct. So the answer to the question to Bruce Arnold is: Yes learn intervals as well. It is useful in combination with hearing within the key.
According to these two, harmony is more valuable when performing, and distance is more valuable when listening. I started to consider the possibility that harmonic training was important for the performer, and distance training for the spectator, but it was immediately obvious that I couldn't make that segregation so simply. Of course, a performer is also a listener. If distance is valuable to the listener, and the performer is listening, how could distance be useless to the performer? I was further perplexed by "Contextual Ear Training", an article about ear training written by Paula Telesco, currently at UMass Lowell Department of Music. She expresses strong contempt for scalar interval training.
One vexing problem for many aural skills teachers is the study of intervals. Do students need to be proficient at identifying random intervals before they can move on to something else? No, I don't believe so. Do they need to be proficient at hearing scale degrees and relationships within the context of a key? Most certainly... Nevertheless, the identification of intervals seems to be a major component of many ear training and sight singing texts, CAI music software, and presumably, most ear training programs. But at the same time, many aural skills teachers question their importance, or the value of the method by which they are most often taught. ...what is the purpose of teaching intervals per se? I would argue that we should instead be teaching students to hear the larger relationships: scale degrees, harmonies, and the affinities of notes for each other. Intervals should be taught and understood only as parts of harmonies, not as discrete units to be recognized in the absence of a tonal context.
Even though Paula rejects scalar ear-training methods, she doesn't deny that distance should be taught. When she describes her method for teaching sight singing, she includes this definition: "intervals are the distances between scale degrees, not isolated events." Of course, she intends for the emphasis to be on scale degrees, since most people don't teach intervals in key context, but I emphasize her strange use of distances as a part of harmonic listening. It's fascinating that her entire paper doggedly promotes harmonic listening as an alternative to traditional relative pitch training, while at the heart of her method she retains the concept of distance, which is the most vital component of traditional training. Why might this be? I didn't find any further clues in her paper. Most likely she doesn't recognize a distinction between harmonic and scalar listening, and doesn't see any contradiction in describing harmonic relationships as "distance", but this still doesn't explain why someone so rabidly harmonic would still think distance an acceptable measure for an interval. Somehow, for some reason, she still perceives a distance in her harmonic intervals.
I began to see an answer as I was playing around with an entertaining Note Finder application on-line. This program shows you notes on a staff and requires you to press the letter keys that correspond to the note. At the office, I can't use it with the sound on, but that didn't deter me from trying it. I started with the treble staff. I found that when the program showed me a note, I instinctively pictured my finger playing it on the piano-- having "seen" the correct piano key, I quickly named the on-screen note. Once I switched to the bass staff, though, I discovered how weak my left-hand comprehension is. I had no sense of "home" for my left hand, except perhaps for my thumb on middle C, and I was very quickly lost. I tried the old "All Cows Eat Grass", but my goal was to know the on-screen note instinctively, not by counting lines. I tried pretending my thumb was on middle C, and pictured my hand reaching for each note on the keyboard in relation to C-- but the further down the note was, especially outside of my hand-span, the harder it was to judge. I tried starting at the middle line, D, and judged each note up or down from there, but that was still too slow; since I couldn't decide which finger belonged on the D, I was constantly disoriented. Finally I decided on F, D, A, and C, as pinkie, ring finger, index finger, and thumb. If any of those four notes showed, I knew them instantly; if the program showed me any other note, I could swiftly imagine which finger was pressing it because of my "home finger" on its nearby note. No note was more than a major third away from the notes I knew. I happily tapped away with this strategy, decreasing my identification time to under a second, when I suddenly stopped in astonishment. Without listening to anything, I had been using distance-based relative pitch!
This boils down to what might be an important argument for distance training: that's how you find the notes when you play. As a pianist, for example, there is a one-to-one relationship between the invisible "distance" of an interval sound and the physical distance that your fingers must travel. When you want to play an octave, you may hear the harmonic "two" of the frequency ratio, but your fingers have to find the interval's "eight". You need to know how far apart those notes are so you can press the right keys. Of course, other instruments have valves and schematics which don't have the same one-to-one physical relationship as the notes of a piano-- but according to Mel Martin (from his article), that is to their detriment.
I am mentioning piano players primarily because it has always been my feeling that they hold the "keys" to the harmonic kingdom. They have the ability to move the harmony as well as see and hear it as no other instrumentalist and I have always held a particular fascination with these players. This is why soloists are consistently advised to have a basic working knowledge of the keyboard so that they may develop this type of ability and bring that to their primary instrument.
You need distance in order to move anywhere, and the piano is blatantly designed to quantify and standardize that distance. On an instrument like the piano, which boasts its one-to-one relationship, harmonic perception becomes physical movement directly. I had been musing about whether it would be advantageous to create an instrument whose keys were organized according to Mathieu's harmonic lattice instead of in a traditional relative scale, but that would probably just be confusing. Your hands move in a physical reality, not an emotional one, and they move through linear distance. You've got to make that connection mentally. You've got to know that a major third is a "five" and a "three" so you can hear it and play it. As Paula suggested, harmony is most probably the distance between scale degrees.
I've spent the past few days gathering information with which to dissect and examine the hypothesis from the previous entry. I looked mainly for facts that could support (or disprove) the idea. Do we make a mental connection between audible interval "distance" and the physical distance on our instrument? It seems that yes, we do make a connection, and no, it's not as simple as my previous entry suggested. Although our minds respond to the distance of an interval with a corresponding physical movement, the mind does not necessarily recognize that movement as a "distance".
When I learned to whistle, last year, my voice teacher asked me how I did it. I proudly explained that I had learned to purse my lips, where before I'd tried to form a circle with them. Yes, she continued, but how do you form the pitches you want? What do you do? I balked in astonishment. Having learned to create the whistling sound, I was instantly able to whistle any pitch I could imagine, perfectly in tune-- but not only did I not know how I was forming each pitch, it hadn't even occurred to me that I didn't know! I walked to the mirror and whistled scales, and only then did I discover how the opening of my lips grew wider or smaller as I lowered or raised the pitch. The diameter of that opening represented a physical distance, and I moved my lips to specific distances that bore direct linear relationships to the pitches I wanted, but I couldn't begin to tell you how many millimeters there were in each movement.
Similarly, our fingers don't seem to recognize physical distance-- but they don't go by absolute position, either. On a day when I had nothing better to do than to read Wired news, I stumbled across a new product developed by The Matias Corporation-- a half-keyboard designed for one-hand typing. Notice how the large white letters are in their normal positions, and the small white letters are the mirror image of the keyboard's right side.

The Matias website has posted research papers demonstrating the effectiveness of the keyboard for people who are touch typists. Although the abstracts of each paper claim that the keyboard works simply because "human hands are symmetrical", the full answer is buried in the section on Hand Symmetry vs Spatial Congruence. In that section they explain, "Half-QWERTY is based on the principle that the human brain controls typing movements according to the finger used, rather than the spatial position of the key." I downloaded their demo program, and I was thrilled to discover that it's absolutely true. I am a touch typist (average 97 wpm, 120 at a sprint) and I found that my left hand knew precisely where to go to find the correct keys. I didn't have to look at the keyboard even once.
For those of you who may not be familiar with the term, "touch typing" refers to a system by which a person is trained to use a consistent fingering on the QWERTY keyboard. Through constant reinforcement, the movements eventually become automatic. Whereas a "hunt-and-peck" typist thinks "I want an R" and then has to find that letter on the keyboard-- every time-- my mind has been trained to know that "R" is index-finger, up-and-to-the-left. The process is effortless; it's as though the letters appear by themselves in response to my thoughts. I am convinced this is directly and completely analogous to perfect pitch musicianship, and I'll explore this parallel later; for the moment, I want to keep your attention on Matias' supposition that the typing movement is accomplished with little regard for the spatial position of the key. It's especially important to recognize that they presuppose their subject is already a touch typist. I can tell you that when I was learning to touch-type, I was very aware of each key's spatial position. An "A" was over here, an "H" was over there, and an exclamation point was... where is it... shift-1. (Extra points for those of you who remember the exclamation point as Shift-8, backspace, period.) Now when I want to type "ah ha!" my fingers travel the distance between the keys without a thought.
Whether or not we are consciously aware of our fingers moving through any kind of physical distance to match an interval, that connection has been made. That's what happened with my whistling, and I suspect that this is what happens with the fingering of a musical instrument. A major sixth, or any other interval, is "mapped" to a specific combination of physical positions, whether that map is literally "six notes away" as on the piano keyboard, or is instead the unique combination of finger and lip positions of a brass player. The distance mapping may not be visually obvious from the way you move on your particular instrument, but it is learned-- and is gradually absorbed into the subconscious.
The Matias people support this point with a direct implication that their work is applicable to musicians. In describing others' research into half-keyboard skills, they deliberately compare the computer keyboard to musical instruments, and insist that the absolute orientation of the fingers is irrelevant in favor of the image mapping.
Gopher, Karis, and Koenig [5] trained subjects on a two-handed chord keyboard and then investigated whether the skill thus acquired transferred to the other hand by mirror image or spatial congruence. Their conclusions suggest that spatial congruence is the dominant mapping. They also tested a third condition, a combination of the two, using keyboards mounted vertically rather than horizontally. ...[but] the combined scheme was actually the equivalent of the mirror image keyboard, but with a vertical rather than flat posture (i.e., with the hands positioned as though playing a saxophone, as opposed to a piano).
If this "mapping" is an accurate description of what happens, then we can take it a little further to explain how harmonic perception can translate into physical motion. Once your fingers have been mapped, it doesn't matter whether you play notes together in a chord or separately in an arpeggio; the notes still bear exactly the same relationship to each other. You don't have to think about your fingers "moving" from point C to point G; you don't even have to think "five steps apart". You think "fifth" harmonically, and thanks to the physical distance mapping your fingers instantly know where to be, regardless of your instrument.
An on-line book about piano practicing seems to agree that this is how it works. It takes full advantage of the mapping phenomenon in its recommendation of how you should tackle a difficult passage, with a strategy amusingly titled "The Chord Attack" (their emphasis).
Let's return to the [left-hand] CGEG quadruplet. If you practice it slowly and then gradually speed it up, you will hit a "speed wall", a speed beyond which everything breaks down and stress builds up. The way to break this speed wall is to play the quadruplet as a single chord (CEG). You have gone from slow speed to infinite speed! Now you only have to learn to slow down, which is easier than speeding up because there is no speed wall when you are slowing down.
The book continues, explaining how to slow down from infinite speed, but the point has been made. The order in which you play the notes doesn't matter; the "movement" between the notes doesn't matter. The mapping is only concerned with the relative positions of your fingers.
But the order does matter, and the movement does matter, or melody would not exist! If the interval between notes is harmonically perceived (eliminating distance perception), and the physical motion becomes subconscious (also voiding distance), how is the melody realized? The Matias website has a clue. They posed the question, "which hand to use?", and I was startled by the wording of their answer:
Given the keyboard described above, we must now decide which hand is 'best' for one-handed typing. In general, we believe this is the non-dominant hand. This would free the more dexterous dominant hand to use a mouse (or other device) to enter spatial information.
If you're using a computer, your dominant hand is moving the mouse through physical space, or defining spatial contours with a pen and tablet. Now think about a piano-- isn't the melody most frequently given to the dominant right hand? Isn't it the dominant hand that most frequently "enters spatial information"? I doubt that this is a coincidence, and I wonder how it extends to other instruments. Could it be that, just as harmonic and distance listening are two different psychological interpretations of the same input, harmonic and distance playing are two different physical expressions of the same output?
I'll have to tackle that question later. For now, at least, the evidence does seem to support the idea that distance training is important for the physical production of music. Whether that production is accomplished through conscious movement or subconscious mapping, the distance between notes appears to be an essential component of musicianship.
Lately I've been working mostly on the Harmonic Drills. I'm intrigued by the fact that it's much easier to invent trigger words for harmonic intervals than for pitches; the interval sounds seem far clearer than the pitch sounds. The augmented fourth sounds distinctly "eerie"; the octave sounds distinctly "thin". Although I did deliberately structure the Harmonic Drills in order to maximize the differences between the tested intervals (to make it easier to distinguish between them from the start) the harmonic sound of any interval is still easier to recognize than the sound of any pitch.
This could be because an interval is composed of two pitches-- just like a language sound. A single frequency of 900Hz is elusive and indescribable, but add a second frequency of 1100Hz and it's clearly recognizable as an "ah" sound. Although you can mistake the mixed frequency for a musical sound, you won't confuse the "ah" with an "ee", which is a combination of 250Hz and 2500Hz. It seems reasonable to assume that our mind is especially good at interpreting two-pitch combinations, but this presents a chicken-and-egg problem. Is it easier to recognize the distinct harmonic identity of an interval because we are so well-trained in combining two pitch frequencies (into language sounds)? Or did we, as a species, decide to pair up pitch frequencies into language sounds because they have such distinct harmonic identities?
Like language sounds, and unlike pitches, the identities of each interval are not only distinct, but consistent. The experience of each interval is consistent enough between listeners that it can be specifically described with confidence. I recognized this consistency myself when I was inventing trigger words for the harmonic intervals. I identified the major sixth as "bittersweet", and then was amused to remember that this interval begins "My Bonnie"-- a song about yearning for a faithful-but-distant lover. Surely the interval was selected to open the song because it immediately evokes the appropriate emotion. I found this fascinating, not only because of the obvious match between the musical sensation and the song's sentiment, but because I had identified the "bittersweet" sensation as a single harmonic sound, not as two notes in sequence. The harmonic effect was unquestionably identical, regardless of whether the notes were played together or separately.
This made me wonder where the harmonic identity is created. Although you'd think there is no harmony when there is only one note, the more I've listened to the harmonic drills, the more it's seemed that the harmony is identified by the top note alone. When I hear the major sixth, if I attend solely to the top note-- or even play it separately from the bottom note-- I can quite clearly hear its "bonnie-ness". And, as I listen to both the ah and ee combinations that I created, it sounds like it's the higher pitch which is "speaking" the vowel sound to me. In fact, if I separate the tones, the lower pitch does not sound like the same vowel, but the higher pitch still does. Then, if I listen to eh as in "bet", whose higher pitch is the same as "ee" (750 + 2500), I get a very different effect. Although the lower pitch is now the one that "speaks" the vowel to me, neither the 750 nor the 2500 pitch sounds like "eh". If I want to hear "eh", I can't just screen out the higher pitch; 750Hz by itself sounds like "aw". When I look at the formant chart, I discover that 2500 and 750 are indeed the high formants of "ee" and "aw", respectively. Whatever the contribution of the lower frequency might be, the higher frequency certainly appears to be the one that carries the defining information.
Unsurprisingly, then, I get the same confusing effect when I play the notes of an interval from high to low in the Harmonic Drills. The top "formant" always claims the unique harmonic identity, and the bottom note is content to remain an indistinct "bottom note". (Could it be that this is yet another reason why an untrained listener hears only the top note of a chord?) If I play the top note repeatedly, to make it my point of reference, and then follow it with the bottom note, I simply lose the harmonic identity altogether. The bottom note refuses to relinquish its role as the informant rather than the informed. Of course, this could be merely because I'm not familiar with the concept of the harmonic inversion, but if so, the fact that I'd have to learn that concept just to be able to reorient myself is telling. Why does this bias exist towards the higher frequency? Could it be as simple as our normal perception of the overtone series, which demands a "base note" for context? Does the bottom note provide the root context, and the top note the meaningful interference?
This apparent top-bias effect provides additional arguments for harmonic and distance interval listening. On the one hand, it's entirely evident that, in harmonic context, each scale degree (as a single note) has a consistently recognizable identity, which is ignored in distance training; but on the other hand, if harmonic identity is muddled when the interval is inverted, you could easily measure the scale steps instead with no regard for the key context. But-- does this mean that distance relative pitch is meaningless in a key context? I still don't have any explanations of why distance perception is supposed to be useful. I've enjoyed speculating about it over the past few entries, but I'm no expert-- despite the appropriate and applicable evidence of the half-keyboard research, the conclusions I've offered so far about distance training are just logical hypotheses. I've been raising a lot of questions (especially in this entry!) and I need some answers instead.
Fortunately, Alain has tipped me off to Ron Gorow's book Hearing and Writing Music. As I thumb through it, I see that this book should be a valuable resource for understanding the supposed merit of interval distance judgment. Ron is an acknowledged expert in ear training (his book has unqualified recommendations from extremely well-respected musicians) and his method is firmly rooted in distance training. I'm especially curious about his methods because one of the bullet points on the back cover says "IN THIS BOOK YOU WILL DISCOVER: Why you don't need 'perfect pitch'."
Today I did a Google search for the phrase "relative pitch" just to see what would turn up. I read some interesting things, but nothing earth-shattering; I didn't keep track of the places I'd visited, which is unfortunate, because tonight I've been wondering about two particular pages that I can't seem to find now. One of them was a reference to an experiment by Ernst Terhardt; in that experiment, by creating unusual testing scenarios, he somehow managed to demonstrate that relative pitch and perfect pitch were equally "innate"-- or equally learned, depending on your point of view. Another was a page which claimed that everyone had to have strong relative pitch, or else they wouldn't recognize the same word if it were spoken by a male or female voice.
I'm curious about both of these pages mainly because I'd like to know whether each of them considered "relative pitch" to be harmony or distance. Did Terhardt's experiment test people's ability to hear harmonic characteristics, or their ability to judge implied motion, or both? Would the results have been different with harmonic testing-- do we have a natural affinity for relative harmony which the experiment ignored? I also have to wonder what the second author had in mind when they said that speech perception required relative pitch; are they suggesting (incorrectly) that this is because the sounds are spoken at different fundamental pitches, or (more accurately) because the speakers' different formant choices bear similar harmonic relationships to each other, or (most plausibly) because every spoken word is a harmonic garble which requires cognitive processing to separate into comprehensible sounds? It seems likely that our ability to perceive words and phonemes is a direct function of harmonic relative-pitch skills. Next time I'll have to be more careful to bookmark my sources-- even if I don't know that they're going to be sources. I'm especially frustrated to have lost the specifics of these two observations, because they feed right into an assertion I've found about phonemic awareness.
Adams (1990) and Blachman (1984) warn that word consciousness (the awareness that spoken language is composed of words) should not be assumed even in children with several years schooling, though they report evidence that it may be readily taught even at a pre-school level. That school age children can lack such fundamental knowledge may be difficult for adults to accept, but it highlights the need in education to assume little, and assess pre-requisite skills carefully.
In other words, sound events which are temporally separate may not be cognitively separated. Perhaps it could be said that our minds simply have a tendency to group continuous sound streams into holistic units? I wonder if the Portuguese illiterates I've mentioned before, who definitely did not possess phonemic awareness, did have "word consciousness". Phase Eight of my research may turn out to be an evaluation of phoneme theory and education. This same webpage I've just quoted has a list of "stages of phonological awareness development", along which the Portuguese illiterates could have progressed as far as stage six or seven and still failed the experimenter's tests.
1. Recognition that sentences are made up of words.
2. Recognition that words can rhyme - then production thereof
3. Recognition that words can begin with the same sound - then production thereof
4. Recognition that words can end with the same sound -then production thereof
5. Recognition that words can have the same medial sound(s) -then production thereof
6. Recognition that words can be broken down into syllables - then production thereof
7. Recognition that words can be broken down into onsets and rimes - then production thereof
8. Recognition that words can be broken down into individual phonemes - then production thereof
9. Recognition that sounds can be deleted from words to make new words - then production thereof
10. Ability to blend sounds to make words
11. Ability to segment words into constituent sounds
I'm operating under the premise that pitches in music are directly parallel to phonemes in language (and words to chords); according to this list, the "recognition that words can be broken down into individual phonemes - then production thereof" is the eighth of eleven total stages. Yet this eighth stage is precisely where all current methods of perfect pitch training begin, skipping over the first seven stages completely in the mad quest to "name notes".
It's true, of course, that some people are perfectly capable of starting at stage eight simply because their existing musicianship and ear training accommodates the first seven stages. Nering's research allows for this probability, since she showed that people got better at naming notes in isolation. The general lack of attention to the first seven stages supports Ron Gorow's statement (from his book), "there are claims that 'anyone can develop perfect pitch.' We maintain that 'almost anyone can develop an approximate pitch memory.'" I would agree, if you amend "...based on available methods" to this quote. Current methods do train for "approximate pitch memory", not for full perfect pitch, because they start in the middle. Stages 1 through 8 are all learning stages, and then you can see how stage 9 through 11 are results which represent, respectively, the abilities to arrange, improvise, and play by ear. I'll need to figure out what the musical parallels are for the first seven stages so we can start at the beginning. It's my theory (and my hope) that by developing a training program which includes the first seven stages, adapting whatever effective strategies have been demonstrated by the phoneme-teaching corporations (Hooked on Phonics, Scientific Learning, and the rest), then learning total perfect pitch perception will become not only easy, but inevitable, for anyone who tries.
Naturally this isn't the entire story; I still need to explore perceptual learning, for one, and if you haven't noticed it yet on my library page, allow me to alert you to a remarkable book. The book is in German language, and is titled Erziehung zum absoluten Gehör, which translates to Education for absolute hearing. It is, astonishingly, what I thought I would have to invent-- a systematic method to teach perfect pitch to children. I don't speak German, but the book is well-illustrated. I don't yet know whether the book's contents will support or contradict my phoneme-learning expectations.
I'm pleased with Hearing and Writing Music, at least in an initial skim. To begin with, Gorow makes a semantic distinction that I hadn't considered. I've been deliberately using the word "note" instead of "tone", just because I prefer the sound of the word "note"-- but Gorow says there's a practical meaning for each word, and I think I'll adopt his terminology from here onward. Specifically,
[M]ake a distinct separation between the hearing process and the writing process... use the word tone only when we're referring to a sound and the word note only when we're referring to a symbol. Think of a tone as perceived through the sense of hearing and a note as perceived through the sense of sight. A tone lives in the air and defines a sense of musical space; a note lives on the music staff and serves to communicate musical thought.
Gorow also makes the corollary point that a musical tone is a four-dimensional object, having specific measurements in both space and time. When I read this, I immediately remembered one of the chapters in Thinking in Sound, which offers specific scientific evidence that a sound's duration is part of its perceived identity. I also thought of the science-fiction concept of hyperdimensionality-- it's an idle thought, since I'm not sure I can do anything with it, but I wondered if one of the reasons it's so difficult to recognize a musical pitch is that our minds aren't accustomed to explicit four-dimensional perception. In any case, I'm pleased with Gorow's simple, but not simplistic, approach to the material. All the emphases in the quote above are his, which is typical of his writing style in this book; and, at one point, he does take the time to tell you in big bold letters that "The fifth is fundamental to all music, the essence of tonality and the origin of Western harmony." I'm looking forward to reading Gorow's justifications for learning intervals by distance.
I'm also expecting many good things from the Absoluten Gehör book, although it will be a while before I bring out those things to you. I'm in the process of retyping the entire book, and translating it one paragraph at a time using freetranslation.com. Although this is certainly not the most efficient way to get a translation of the book, I will become quite intimate with the material, as I must understand the ideas in order to correctly interpret the grammatical hash provided by the website. I have chosen to retype the book rather than scan it for OCR; in addition to this process actually being faster (since, for me, proofreading an OCR'd file takes about as much time as typing it from scratch), I'm discovering some fascinating things about the psychology of touch typing. I'll have to explore these later in comparison to musical performance. For just one example, my fingers keep wanting to add letters that aren't there. When I see "relativ" I have to consciously stop myself from typing "relative", and I don't usually succeed. Or I see the word "sind", but my fingers give me "since"-- this effect happens in the middle of words, too, and I honestly don't know what familiar letter combinations my mind is noticing (and trying to complete in English). I correct them too quickly to realize what I'm doing. Trying to type swiftly in German is bringing out all kinds of invisible mental assumptions that I make when I'm typing in English, and I'm sure these will be important statements about how our minds and fingers connect in musical performance, and how we mentally organize language-sound information in its physical (re)production. I'll have to visit these observations later, when I've finished all 99 pages of the book.
Before Gorow approaches absolute pitch, he gives his rationale for learning relative pitch. He explains how everything in music can be varied, including pitch, key, tempo, dynamics, temperament, and timbre-- everything, that is, except the interval. "The interval is the only constant in music... it is, by definition, a fixed ratio." As long as its intervals are maintained, a melody retains its complete identity; so to truly understand music, all you need to learn are intervals.
To dismiss the importance of pitch sensation, Gorow makes the following statements (the numbering is mine, just for convenience):
1. A single tone... does not convey much... emotion or thought.*
2. Pitch is arbitrary.
3. Key is arbitrary.
4. [A song] sounds the same in any key.
I had to figure out what Gorow meant by "pitch is arbitrary." His two reasons are these: standard concert pitch has varied through history, and as an orchestra tunes up and warms up together their pitch may change. Based on these two reasons, it's clear that he's really saying "the selection of pitches or frequencies represented by note-names is arbitrary" (and he does say that, six pages later), and this is undeniably true.
It was easier to understand what he meant by "key is arbitrary". According to Gorow, key signature (and, by extension, pitch choice) is purely functional. "The choice of pitch/key is orchestrational, rather than compositional," he says, "determined by considerations of vocal or instrumental register." In other words, the only reason to use any particular key signature is to accommodate the instruments you want to include. Now, if you accept that this is true, then you immediately have to ask the question, why would you choose one instrument versus another? A clarinet may happen to play in B-flat, or C, or E-flat; you would undoubtedly select one of them because each has a different emotional impact. Yet in choosing a specific instrument, what you are choosing is a specific key signature with a predictable pitch template. Which is to blame for this difference in emotional effect-- the instrument, or its key signature? Gorow is indicating it's the instrument.
Gorow appears to explicitly deny that different key signatures have different "feelings", ascribing all emotional content to the melodic contour instead. "What is melody but a sequence of intervals and rhythms? (Oh, but what a sequence when a melody resonates your emotions!)" Now, if the melody is all that matters, his statement logically follows that "[a] melody may be sung or played at any pitch, in any key, and it retains its melodic shape, its identity." Continuing this logic-- if a song's identity is entirely its melodic shape, and the composer's choice of key signature depends entirely on the instrument, then key signature in piano compositions must be totally irrelevant. The composer might as well have picked the key out of a hat. Although it might seem strange to think that key signature on a piano is meaningless, it seems to be a fairly common expectation. A few months ago, I was surprised when my friend Craig Shaynak, a highly skilled jazz pianist and improviser, expressed his genuine amazement in discovering that a melody played in a different key "felt differently". In his many years of playing, Craig had never thought to listen for this before. Whether or not Gorow is aware of this feeling-difference, Gorow's stated conclusion is that key difference is entirely unimportant to musical perception.
So if you tie this together, Gorow teaches you that musical identity is wholly defined as melody, which is defined as a succession of intervals, which are defined as distances. I find the negative assumptions here quite striking:
Key signatures are unimportant.
Pitches have no identity.
Context is irrelevant to harmony.
Harmony is irrelevant to melody.
Whether or not you agree with these assumptions, they do combine to provide us with the first and perhaps most compelling reason for learning intervals by distance: for any type of interval, the distance between pitches never changes. Regardless of the context, irrespective of the key signature, no matter what pitches are used, an interval's distance is inalterable. If you can judge distance, you will always and infallibly recognize any interval.
*Although he certainly didn't intend this, I feel obliged to compare this statement of Gorow's to the anecdote he uses to open Chapter 3 of his book: "A music student sat in the audience, eager to hear his first composition. The piece opened with a single tone, a cello sustaining the low C string. The young composer was heard to utter, 'Wow, did I write that?'"
In Hearing and Writing Music, for two pages, Ron Gorow discusses why you don't need absolute pitch, and how having it would be harmful to your musicianship. In this section, titled "Absolute Pitch vs. Relative Pitch," his arguments seem logical, compelling, and reasonable-- if you accept his definition of perfect pitch:
Absolute pitch is the ability to identify tones; relative pitch is the ability to identify intervals. (page 70)
I wonder what Gorow would think of the research I've been doing? My research disagrees with his definition. I'd have to say that absolute pitch is the ability to recognize the unique quality of a pitch, and suggest that all the popular "definitions" of perfect pitch-- the ability to name, memorize, recognize, etc-- are side effects, not the root ability. Would this change his mind?
I suspect that in order for anyone who has had traditional ear training to accept a new definition, he would have to change his entire philosophy of music, and abandon the assumptions I noted in my previous entry. Those assumptions aren't exaggerations. Gorow says that pitch and key are merely a "mechanical apparatus" which has little bearing on the musical experience. "Free yourself to be able to hear music in its organic state," Gorow urges, "without reference to specific pitches." (p 71) I doubt that this kind of belief could be argued away; you'd have to feel the difference for yourself before you'd think differently.
It is tempting for me to see "Absolute pitch vs. relative pitch" as a challenge, and launch a defense for every minor point. But the fact is that all Gorow's arguments stem from his definition, and if you change that definition the arguments are no longer applicable. Additionally, Gorow presents absolute pitch versus relative pitch, as though they were exclusive of each other. In order to respond point-for-point, I'd have to agree to that perspective too, and I don't.
For example, Gorow says that "with relative pitch, you can easily listen in one key and notate in another key." This is a true statement; but, as Rich has noted, you can do that with relative pitch by thinking either "minor second up" or "sol to le". When you listen harmonically, distance is optional-- and, contrary to Gorow's complaint, absolute pitch doesn't interfere. All Gorow's examples against perfect pitch are like this; what he says is true and correct, but if you change the premise you get a different result. In that respect, Gorow's statements about absolute versus relative pitch turn out to be neither an argument for learning interval distance, nor an argument against perfect pitch. They're simply comments about the benefits of ear training.
As I've been retyping Erziehung zum absoluten Gehör, I've been noticing how my fingers and hands behave. There have been many curious results. For example, unless I'm extremely tired, my right hand is "alive". It tries to lift itself from the keyboard, and make conscious fingering decisions for each letter, trying to be aware of each choice, actively seeking each new key. Ironically, this mindfulness invariably slows down the process by a large factor. Regardless of my energy state, though, my left hand always remains "dead" as it sits low on the keyboard. It's dully content to stay rooted on the home row; it mechanically reaches for the proper letters without any conscious interest whatsoever. I don't think it's a coincidence that the "extended keys" of the keyboard are located on the right side; the right hand is much more willing to leap up into a new function and a new position.
This and other observations I've noted mentally-- I'm sure I'll get back to them later-- but I've been specifically cataloguing my typographical errors. The typos fall into four categories almost exclusively: same-finger errors, letter transposition, bad completions, and sound substitution. (There were a couple times when I did hit a completely incorrect key, for no apparent reason, but that's happened so infrequently that I've been unable to identify a pattern, or to have noticed what I'm thinking when I do it.)
Same-finger errors have been my least common mistake. I only did this a few times-- typing "sollren" instead of "sollten", or "bedürgnis" instead of "bedürfnis". I used the correct finger but pressed the wrong key. In the half-keyboard research, this was their most common type of mistake, but that can be explained by the simple fact that the typing task is different. (In fact, I've made quite a few same-finger errors typing this paragraph right now!) But, common or uncommon, it's worth noticing that this kind of error exists. It supports their theory of finger-choice instead of absolute-position mapping, and strongly suggests that the spatial position of keys on your instrument is not important.
Letter transposition is swapping two letters around. As I tracked this type of error, I made note of when I recognized each mistake; in every instance, I noticed the error at the end of a syllable. When I read "Entfernung", I typed "Entef" and stopped; I saw "Hauptbestandteil" and typed "Haput" before I caught myself. I typed all the letters of a syllable before recognizing the problem. The psychology seems obscure in the examples, as it appears I merely stopped after typing the wrong letters; but I assure you that I intentionally typed "En-tef" and "Ha-put", not "Ent-fer" and "Haupt". I made many transpositions just because I had perceived the wrong syllables to begin with-- but whether or not I had the correct syllable, I'd always type the entire syllable before acknowledging my mistake. The transposition error may occur, then, because a syllable is perceived as an instantaneous unit, and all its letters are remembered as a single specific shape. This supports the principle of the "chord attack" from the on-line book about piano practicing, and also reflects the idea that we comprehend the phonemes of a word simultaneously, instead of as an ordered sequence. When I see the word "einmal", my mind creates the syllabic units "EIN" and "MAL". Then, like the chord attack, my fingers have to slow down each three-letter "chord" from infinite speed to words-per-minute-- and the letters don't always come out in the correct order. (Unfortunately, I wasn't able to track most of my transposition errors, because I noticed them almost subconsciously. I could feel that I'd made the mistake, and my fingers automatically leapt to CTRL-backspace, deleting the entire word, and I'd completely retyped the word and moved on before I even recognized that I'd done something wrong. I suspect the automatic nature of this response may be significant.)
Bad completions are those where I saw the German word but typed a familiar letter combination instead. This has happened all over the place. Here are a few of them:
|
I saw |
I typed |
|
sind |
since |
| absolut | absolute |
| relativ | relative |
| als | also |
| sein | sine |
| Farbpunkten | Farmpunkten |
| stattfindet | stattfinger |
| Darauffolgende | Dararuffolgende |
| unbefriedigend | unbefriendigend |
| Kalender | Kalendar |
| individuelle | individualle |
| organisatorisch | organizatorisch |
| gehorbildung | gehorbuildung |
The bad-completion error lends additional support to the idea of multiple letters as instantaneous "chords"; there's no better explanation for "stattfinger" than to acknowledge that I've learned "finger" as the complete shape which is prompted by "f-i-n". I was intrigued to discover that, of all the errors, bad completion is the most susceptible to new learning. After typing "wiederhold" instead of "wiederholt" nearly a dozen times, I saw the word "wiederholen" and typed "wiederholden" instead. And, after typing the "äch" sound so often, I inadvertently typed "allmächlich" where I should have written "allmählich".
This error also demonstrates that you produce specific letter/concept associations based on the language you're thinking in. I saw "Kalender" and "individuelle", but interpreted and reproduced them as the semi-English words "kalendar" and "individualle". My mind believed that these different spellings were substantially identical. And why shouldn't I think so? The letters have the same relationships to each other in each word; when you pronounce the words out loud, they sound almost exactly the same. Relatively, they are identical. But a German speaker would look at each one and instantly know which letters were wrong. I imagine that this effect has its parallel in musicians who play predominantly in a single genre-- a jazz musician has internalized certain expectations of phrasing and progression, which are different from a classical musician's, which may be different from rock, et cetera. The note relationships are recognizably identical, but each pattern of relationships is readily identifiable as belonging to its genre. You may not be consciously aware of the difference unless you can perceive its absolute sound.
This brings us to my single most common typing error: sound substitution. I'd look at the page, and "hear" what I saw; then my fingers reproduced the sound in my own language-- and dialect. Here are just a handful of the many, many examples. As you'll notice, I didn't always "hear" the original word correctly.
|
I saw |
I typed |
|
Lernen |
Lernin |
| für | fir |
| sich | sick |
| Umgekehrt | Umgekehert |
| schlecht | schlect |
| Gegenstand | Gegunstand |
| bewerkstelligen | bewerkstellighen |
| wenig | weneg |
| Baßschlüssels | Baßchlüssels |
| neue | newe |
This error, and the sheer number of times I made it, represents the most critical point-- your mind uses the keyboard to reproduce the sounds you're "hearing", not the symbols you're looking at. The other errors demonstrate this too, but not as vividly. The last word in this list, "neue", is especially remarkable, because I spotted it about three sentences in advance. The moment I saw it, I consciously told myself "look out for that, make sure you type it correctly." As I approached the word, I reminded myself "Now here it comes, get ready," but then as soon as I reached it, my fingers went ahead and typed "newe" anyway. (Has this ever happened to you on your own instrument?) There is some evidence that symbol-sound associative learning occurs, which is encouraging for perfect pitch study; I eventually heard the ß correctly as "ss", instead of "B". This is why my mind automatically omitted the redundant single "s" from "Baßschlüssels". I would not have made that error if I had not looked at the symbol "ß" and heard the "ss" sound in my mind.
All of this leads to the important question: in music, what happens if looking at a symbol causes you to hear nothing? I introduce this question in direct response to Ron Gorow, whose opinion seems to encapsulate a popular conception of perfect pitch. In his section "Absolute pitch vs. relative pitch", after providing his definitions of each, he begins with this paragraph.
Since the perception of music has relevance only in the abstract, in terms of intervals, musicians possessing absolute or "perfect" pitch have only one advantage: a built-in pitch reference. If you don't have absolute pitch, have confidence that you are not handicapped; a 1 oz. tuning fork will provide you with "absolute" pitch. (p 70)
I'll illustrate this situation as Gorow describes it here: you see a piece of music that starts on a B-flat. However, that note on the page triggers no sound in your head. So you strike a tuning fork to hear an A; you move that "up one-half step", and ah! Now you can follow the music from interval to interval, and even hear all the chords properly in your head. Yes, in this respect, Ron Gorow is right; you don't need perfect pitch if you have a tuning fork. But I must make two points.
First, this reinterpretation of the same situation: You looked at a printed symbol which represented a specific, fixed sound, and you could neither bring that sound to mind nor reproduce it with your voice. You could not "read" the symbol. There is a word for this condition. It's called illiteracy. If you showed this same lack of aural/verbal response to letter symbols-- even if you spoke the language perfectly well in conversation!-- people would think there was something wrong with your education (or your intelligence). If I were to advance any single argument for learning perfect pitch, this is it. Perfect pitch allows you to "read" music correctly, completely divorced of any external assistance. You look at the symbols, and you instantly hear the sounds in your head, just like reading a language. Perfect pitch makes you musically literate. Yes, I'm aware that there are talented composers (like Paul McCartney) who have perfect pitch and can't read sheet music-- but there is also such a thing as a talented but illiterate poet. Which do you want to be?
Second, I'll ask you to consider what Gorow is saying to you by analogy to language. If you're old enough, you remember the Texas Instruments Speak & Spell.

This was my favorite toy in third grade (1979-80; it was brand new at the time). Each time you pressed a letter, it said that letter out loud, and I enjoyed making it say all the word spellings. I was especially fond of the B, which sounded like the speaker's lips were exploding (I've since realized that this was deliberate, to differentiate it from the V). Essentially, the Speak & Spell is a "tuning fork" for letter sounds.
Now, think of the things you read every day. Imagine what it would be like if every time you looked at a sign, every time you picked up a book, every time you glanced at a headline, you couldn't read it until you'd pressed its first letter on your Speak & Spell? And then, if you happened to look away and lose your place, wouldn't you have to come back to the Speak & Spell before you could start reading again? This may seem a bit silly, but that's the point. It should be this obvious that not having perfect pitch means being unable to "read" music.
But this is not an argument against relative pitch. Even in this same analogy, a Speak & Spell will not help you with word divisions, consonant blends, vowel substitutions, and all kinds of linguistic features which can only be compared to relative pitch. I am attempting to illustrate, first of all, that knowing each pitch sound is as surely a component of reading music as knowing each letter sound is a component of reading language. Without this knowledge, you can't read, and you can't write, without a crutch to help you. Yes, using that crutch, you can do extremely well-- but why settle for that? You can and should have both. Clint, who runs the Prolobe site for perfect pitch training, says it well:
In your last entry, you had a disagreement with Gorow's view that AP and RP are exclusive. I just wanted to support your view on this and maybe add a theory of why he'd believe the contrary. I myself have not lost any form of RP in my development of AP. For me it's like adding AP to my listening abilities. Gorow could have been looking at individuals who were born with AP and neglected their RP because of it. I know individuals with AP who have the inabilities that are commonly easy for people with strong RP. When looking at these people it would be easy to say RP is way better. Without knowing that both could be found in people as well, one might think they are exclusive.
I'll make one more parallel between musicianship and typing-- but before I do that, I suppose I should remind you (although it may be entirely obvious) that everything I'm saying here is predicated on the hypothesis that people with absolute pitch perceive pitch sounds as though they were language phonemes. If you don't agree with this, you may not agree with anything I'm saying; I'd encourage you to read the rest of this website to see what led me to this conclusion. If you still don't agree, by all means write to me and tell me why. I find the evidence rather compelling, but it's important to hear challenges and alternate interpretations.
The last parallel is that of memorizing musical pieces. Whether you're a touch typist or not, consider how you'd respond if someone said to you "Please type 'the cat sat on the mat.'" In your mind, you would first think of "the", and break that into "t-h-e". Then you would look for "t, h, e" on the keyboard, and press those keys. You'd do the same for c-a-t, s-a-t, and so on. But get this: you've already memorized the entire passage. If the same person said to you the next day, "Could you type that sentence again?" you could sit down and do it, even if you had to pick out the keys one by one (again). Just think about what it would be like if you couldn't hear the sentence in your head, and decide which is easier: remembering one sentence-- six words which logically follow each other to form a single concept-- or remembering the spatial positions of eighteen keys? If you have perfect pitch, or well-developed relative pitch, or (especially) both, the language/sound memory automatically tells you which keys to press. That's the way it works; my typing errors show it too. If you have neither perfect nor relative pitch, then you must memorize keystrokes. Why waste your time?
I'll offer one final thought about typing, which was the seed of today's entry. About three years ago, before I had begun any of my research, I had a cheap electronic keyboard with a cheap electronic sound. Craig came by to visit; he sat down on its bench and began improvising. As beautiful sounds and clever harmonies gushed forth from this banged-up box, I was especially entranced by how ordinary, almost mechanical, Craig's hand motions appeared to be. Geez, it looks like he's just typing!, I thought. If you have the chance, take some time to watch a skilled touch typist, and then watch a skilled pianist improvise on his instrument. You'll find that their movements look almost identical.
It's been pointed out to me that there's a Gorow quote I've already mentioned, with which I can draw another analogy to written language. In trying to explain why pitch recognition is not important, he says "a single tone does not convey much emotion or thought." That's true... but neither does a single letter of the alphabet (except X, maybe), and we drill those into our children's heads. Not much emotion or thought in the letter P, so why bother to learn it? [Maybe that's part of why Sesame Street has been so effective over the years-- I remember puppets going crazy with delight for the letter J.] Now... although Gorow begins his ear training book with his thoughts about absolute pitch, I might have made a tactical error in making that topic my first exposure of his book to you. Gorow is an acknowledged ear-training expert (you should see all the big names who have recommended his work); I bought the book to talk about what he does know, not what he doesn't know, and what he does know is substantial. I may have had a field day with what I contend is his misunderstanding of perfect pitch, and I think that discussion has illustrated some important concepts, but I want you to keep in mind that his "Absolute pitch versus relative pitch" is only two pages of his 431-page publication. My research disagrees with his philosophy, but I still want to know more about the expected benefits of his style of relative training.
However, a few things have come up first.
In another interesting conversation with Lisa Popeil (over the phone), she confirmed to me that when people ask her how she sight-reads, she always tells them that "I type the notes that I see." Having mentioned that it looks like typing, I'm glad to know that it feels like typing, too. After we hung up, I was thinking about how that must be different from typing words... the main difference seemed to be that when you see a chord, you have to type the pitches all at once, instead of in sequence. That would be much harder, I thought, because you'd have to apprehend each new chord immediately, and quickly move all of your fingers to a completely new configuration. If chords were like words, surely that'd be like typing 200wpm!
But I suddenly realized how that fit in with my previous entry. After all, hadn't I just finished explaining how our mind "knows" all the letters of a word as a single shape? I sat down at the computer keyboard, looked at some printed text, and began to retype the text-- but instead of attempting to type them as letters in sequence, I tried to hit all the keys of each word simultaneously. And sure enough, it worked. To the extent that it was physically possible, it worked. Piano music is written to accommodate the instrument; the composer knows that each finger can only press one note at a time, and the keys are laid out in a line so that you don't get tangled up. On the computer keyboard, you often use the same finger for different letters in a word, and since you're expected to move your hands while typing you can't easily press certain combinations without contortion.
Entertained, I continued my "chord typing" for a while. Since I was able to type a complete word instantly (when the keyboard configuration allowed), it seemed extremely plausible that someone would see a sequence of chords and be able to quickly type them one after another. The limitations of the computer keyboard even revealed some of my subconscious strategies. With the computer keyboard, for example, when I saw the word "simultaneous", my fingers automatically placed themselves on the letters S,I,M,L,E. I slowly began to type the word, and discovered that each finger had jumped to the first letter that it was going to press. My middle left finger had gone for the E immediately, even though it was going to have to wait for T, A, and N, because that was the word's first letter for that finger-- and also because (somehow!) I had known that the finger would not have to move out of the way for any of the other letters. I noticed that by placing my fingers on S and E, my pinkie was left on the first letter it was going to type (A), even though I hadn't been aware of its moving there. Had I done this on purpose? Since the A was a home key, I wasn't sure. In any case, it seems extremely likely that with the proper ear training and knowledge of music theory, the mental strategies I use for touch typing would be fully applicable to playing a musical instrument.
That should be enough about typing, for now. The other thing that's come up, by whatever wonderful coincidence, is Time magazine's cover story this week, which is about dyslexia. It's unfortunate that I can't just reprint the entire feature here, nor can I link directly to it because it will cycle into Time's archives in a very short while. I'll encourage you to read my previous entry, and keep it in mind while you go check out the article; I'll be commenting on it soon.
At this point, I consider the following structures to be psychologically identical (update 5/5/6 - this chart has changed so that I believe a phoneme is an interval, and a pitch is a subphoneme... or hyperphoneme, depending on your point of view).
|
Language |
Music |
|
phoneme |
pitch |
| syllable | chord |
| word | progression |
| sentence | phrase |
From my research and observations to date, it seems that anything we can learn about the psychology of each linguistic unit is directly applicable to its parallel structure in music. This is important principally because, if it is true, we can expect to teach musical ear training and comprehension using the exact same strategies as those which have been developed, tested, and proven for language and reading acquisition. The questions become: what are the musical training goals? And which learning models do we use to reach those goals?
As I've mentioned, I found the overall journey laid out most concisely on the website about phonemic awareness. Their six steps describe the complete process, from beginning to end-- each step as a giant leap.
1. Phonemic awareness
2. Letter-word correspondence skills
3. Fluent word recognition
4. Vocabulary
5. Comprehension skills
6. Appreciation of literature
By "giant leap" I mean that each of these steps represents a goal that is reached by a series of training objectives. The first step alone, for example, is broken down (by the same website) into the following steps:
1. Recognition that sentences are made up of words.
2. Recognition that words can rhyme - then production thereof
3. Recognition that words can begin with the same sound - then production thereof
4. Recognition that words can end with the same sound -then production thereof
5. Recognition that words can have the same medial sound(s) -then production thereof
6. Recognition that words can be broken down into syllables - then production thereof
7. Recognition that words can be broken down into onsets and rimes - then production thereof
8. Recognition that words can be broken down into individual phonemes - then production thereof
9. Recognition that sounds can be deleted from words to make new words - then production thereof
10. Ability to blend sounds to make words
11. Ability to segment words into constituent sounds
When I presented this list to you before, I pointed out that existing perfect pitch education works on step #8 (with Pitch Acuity Drills), and fails to provide training for any of the other steps. This time I want you to notice something else-- nowhere in this list will you find "learning the sounds of the individual phonemes". The process of learning the pitches is altogether separate from total "phonemic awareness".
So how does the pitch-learning process work? Perhaps we move through "levels of perfect pitch" reported by Marguerite Nering:
1. the subject notices but is unable to identify the tone color
2. the subject recognizes the notes on his or her primary instrument
3. the subject is to detect sharpness or flatness of a tone on his or her primary instrument
4. the ability to discriminate between the twelve tones on any musical instrument
5. the subject is to detect sharpness or flatness of a tone on any instrument
6. ability to aurally recall any of the twelve semitones with no objective reference
This is an interesting contrast to Taneda's levels of perfect pitch from Erziehung zum absoluten Gehör. Although both authors' lists end up in the same place, Taneda arrives by a different route. The most important difference between these lists, though, is that Nering's levels seem to emphasize the instrument timbre, while Taneda highlights the octave spread. Here's how Taneda describes it.
1. Absolute hearing of a single sound
2. Absolute hearing of several sounds
3. Absolute hearing of C-major sounds in narrow area
4. Absolute hearing of all C-major sounds
5. Absolute hearing of all sounds in limited circumference
6. Condition-contingent absolute hearing (dependent on how you feel that day)
7. Timbre-contingent absolute hearing (dependent on your instrument)
8. Composition-contingent absolute hearing (related to certain songs)
9. Complete absolute pitch (able to identify notes)
10. Active complete absolute pitch (able to recall and reproduce notes)
Although the two lists are otherwise substantially similar, Taneda's perspective suggests at least two training modifications to make pitch identification easier. One, by working with multiple instruments, you can eliminate contingency #7; and two, you can improve your training by working first within a "narrow area" of pitch height and expanding outward later.
But in both cases, their ultimate training goal is to teach you to hear and recall twelve different pitches. If you're able to recognize and recall the twelve notes of the chromatic scale, you supposedly "have perfect pitch". But as you can see, there is no overlap whatsoever between these "levels" (on either list) and the progression of phonemic awareness. You can have perfect pitch, according to the classic definition, and still be entirely unable to recognize any pitches within music, because in terms of phonemic awareness you never trained for any of the levels-- except #8, which (as practiced) works in isolation from music. Because your mind naturally perceives musical constructs as having their own unique identity, independent of their component pitches, you can't recognize the pitches inside of the music, even when you know all twelve notes perfectly well. Gorow's material does suggest-- and it seems psychologically true-- that your mind considers the pitches to be meaningless in favor of the musical structure. In order to change this, you need to gain phonemic awareness in music.
The illustrations in Taneda's book make me think he may be aware of this fact, but I haven't yet decoded his explanations to be sure. Here is a reproduction of one of those illustrations, which I imagine could potentially be an exercise to create "recognition that [chords] can have the same medial sound" (#5). Perhaps this and other of Taneda's exercises are meant to increase phonemic awareness, but I haven't translated enough of the book to know.

To address the ten levels of phonemic awareness (in addition to what I may find in the Taneda book), I have been expecting to follow the phonemic-learning models presented by companies like Scientific Learning and Hooked on Phonics, and couple those strategies with principles of perceptual learning. I am anticipating finding ways to make chords "rhyme", and ways to construct "sentences" which expressly highlight and emphasize the pitches being worked on (each of them shown variably as beginning, onset, rime, et cetera), along with exercises to blend, separate, and substitute in different contexts. I've figured that I will want to invent as many different ways to hear a pitch as possible, and I've surmised that this-- in theory-- would make it far easier to learn perfect pitch from the ground up.
I now have strong validation of this theory, in the form of a letter from Mon in Australia. He recently wrote to me about his own ear training experience, following up the conversation we'd had on May 16. This is what he said (with some light editing for length).
I'd like to say that I've made considerable progress since we last spoke and I'm much closer to what I think is having perfect pitch. Last time we spoke, we were talking about the "cat analogy". So I pursued that approach and included arpeggios in my training. The side effect was that it improved my perception of pitches and I can now hear the pitches "phonemically" instead of "melodically" [which was] how I've BEEN HEARING THEM ALL MY LIFE. I think the reason why a tonal center shifts is because most of us have been taught the pitches in melodic form. We were taught songs in class and were taught melodies. Even the notes were taught as melodies; "Re" in the key of "F" is "G", but the "F" scale sounds like "do re mi fa so...etc". That's why when I press "C" on the keyboard, I hear it as "Do" in the key of "C"; when I then hear a song in another key, the "Do" has moved and "C" sounds so different. This is why during isolated note training, when the computer inadvertently makes a progression of pitches that make up a scale in another key, my tonal center moves because I hear the pitches as a melody instead of as phonemes.
Now that I can hear pitches phonemically, I've found that pitches don't move and to some extent have distinguished the phoneme from the overlap when I hear the pitch in an arpeggio or a chord. The pitch remains the same! The side effect is that now, I can tell what pitch an everyday ordinary sound like a bell sound is, or the pitch of the ring tone of the phone, or the pitch of the ambulance siren.
Having said all that, it doesn't mean that I have achieved perfect pitch. At least not yet, because I still hear pitches melodically and it's something that I need to "un-learn". But I think that more training will get me there. Now I'm sure you're gonna ask what's it like to hear "phonemically" instead of "melodically"? Well, let me first tell you what it's not. It's not hearing a pitch and comparing it with something. There is NO comparison involved whatsoever. You either know it or you don't. It's like looking at a color and saying that it's red without comparing it to blue. it's not memorizing it but learning it or maybe getting familiar with it. ...I may have learned to identify all 12 pitches in isolation but it doesn't mean that I've learned them "phonemically". I may have learned to identify them in the key of "C" but if they are still melodic; I will get confused when I hear them in another key. So basically, when I hear a pitch, either I know it or I don't. The minute I figure it out by comparing it with something, it means I still heard it as a melody and not as a phoneme.
So how do you learn to hear a pitch in its phoneme form? I'd say the same way you learn a new word. Use it in a sentence. In music, use a pitch in a chord and/or an arpeggio and play in different keys. You will notice in the first few arpeggios, the pitch seems to change but as you keep doing it, you'll find that it doesn't. Perhaps the brain neurons need to align themselves or something to let you hear the phonemic form.
I found that when I hear a pitch and can't identify it, it's better to say "I don't know" than try to work it out by comparing it with pitch references. I found that if I keep playing the un-identified pitch repeatedly, the phoneme would surface and I could then identify it. it takes a while but practice should make it second nature. When it gets second nature, it doesn't require any thinking at all.
(I then asked Mon if he could be more specific about his process, so I could share it with you, and he elaborated:)
Originally, I played an arpeggio and try to name all the notes I played. The notes seemed to sound different when played by itself than it was when played in an arpeggio; so I tried to investigate how I could hear the note the same way any way it's played so I decided to learn the note individually by trying to find out how it is REALLY unique. Say for example that I'd like to learn Bb; I play an arpeggio of C7 and note how Bb sounds in it. Then I play another arpeggio in Bb and also noting the sound of the pitch of Bb. [I could] play Fsus4, Gm, and anything; just make sure that it has a Bb note in it. I found that during the first tries, Bb seems to change depending on what key it was played in. But as I got used to it, the pitch stopped sounding different. Also, I invented an exercise just for learning a particular note... playing Bb in different octaves, tempo and velocity. ...I play other notes that blend with it and also that would be dissonant with it to act as a vaccine (as I would call it) to make my ears immune to the things that would cause the Bb to sound different. ...What I found was that somewhere in the center of the note/pitch (whatever), is a pure sound that makes its character. If you listen in just the right way, you'll hear it. the next hurdle is to keep hearing it all the time. Learning the association is easy. The constant hearing of this pure sound is what you train for.
His experience, and his description of that experience, make me confident that I've been heading in the right direction. I was especially pleased that his explanation resembles what I'd been saying as early as August 20 of last year. I'm intrigued by his insistence that, when training, he makes no comparisons in order to hear things phonemically; although of course he is comparing the note to itself, in different contexts, I wonder what this might say about the need to compare pitch sensations to each other. Is it an alternative strategy, is it a necessary supplement, or is it totally unnecessary? In any case, Mon has clearly demonstrated that contextual strategies are effective for phonemic awareness, and I am even more confident in continuing to develop the curriculum in this direction.
However, even after Mon's encouraging report, I still had to face an important fact. Phonemic awareness is only step one of six in musical comprehension-- and this first step is itself a giant leap. If I have the models and theories that I need to begin assembling an advanced curriculum for step one, how could I move on to step two, and beyond? The only clue that I seemed to have, inferred from the Scientific Learning website, is that people who can't read music are psychologically similar to people who can't read language. I pondered this for a few days, until I was caught entirely by surprise by this week's cover story in Time magazine-- a special feature about dyslexia.
I only began reading the article ("The New Science of Dyslexia", written by Christine Gorman) to pass the time-- but since phonemic awareness had been on my mind, its opening paragraph grabbed my attention like an explosion of dynamite.
When Sean Slattery, 17, looks at a page of text, he can see the letters. He can tell you the letters' names. He can even tell you what sounds those letters make. But it often takes a while for the articulate high school student from Simi Valley, Calif., to tell you what words those letters form.
All you have to do is replace the word "letter" with "pitch", and this article precisely describes my problem. How do I bridge the gap between pitch-phonemic awareness and musical comprehension? Once you can identify all the pitches, how do you move further and integrate that skill into full (musical) reading comprehension?
As I began reading, I realized something I might have already inferred from the Scientific Learning site-- musical ear-training methods for adults should probably be designed as though the student is learning-disabled. By 17 years old, the person should already be fully competent in musical reading and writing, just like they're expected to be in language. Anything less than total competence means that the person is developmentally stunted, and the curriculum should reflect that fact. Stating the case so harshly makes it clear why there is a stigma attached to dyslexia-- "developmentally stunted" is not a term you'd want spoken about yourself-- but it also creates an analogous argument for the importance of early musical ear training.
No, people with dyslexia are not brain damaged. Brain scans show their cerebrums are perfectly normal, if not extraordinary... But a growing body of scientific evidence suggests there is a glitch in the neurological wiring of dyslexics that makes reading extremely difficult for them. Fortunately, the science also points to new strategies for overcoming the glitch. The most successful programs focus on strengthening the brain's aptitude for linking letters to the sounds they represent. (More later on why that matters.) Some studies suggest that the right kinds of instruction provided early enough may rewire the brain so thoroughly that the neurological glitch disappears entirely.
If I'm understanding that title and this passage correctly, then up until this very year, the popular scientific understanding of dyslexia was that dyslexics were born with dyslexic brains. It was widely known that there wasn't merely a "tendency" for dyslexia, which could be overcome by effective education; people were "born with" dyslexia and couldn't be helped. It was a genetic issue, not a learning issue. If this misunderstanding about dyslexia could have persisted for nearly a century, and its true nature is only now coming to light, then surely we're on the cusp of seeing a similar public revelation for perfect pitch-- finally destroying the "born with" myth of perfect pitch. Dyslexia is a "neurological glitch" that can be completely eliminated; the public should soon learn that pitch anomia can also be educated into oblivion.
Reading requires your brain to rejigger its visual and speech processors in such a way that artificial markings, such as the letters on a piece of paper, become linked to the sounds they represent. It's not enough simply to hear and understand different words. Your brain has to pull them apart into their constituent sounds, or phonemes. When you see the written word cat, your brain must hear the sounds /k/ ... /a/... /t/ and associate the result with an animal that purrs.
Again, if you replace "letters" and "phonemes" with "pitches", and replace "words" with "progressions", you get an interesting statement: In order to read music, "it's not enough to simply hear and understand different progressions. Your brain has to pull them apart into their constituent pitches." I want to emphasize that this "pulling apart" is necessary in order to read, not to play or to listen, because language is perceived in words and syllables. For some reason, Gorman is also omitting here the point that she'll make later-- that you don't actually hear the sounds "k-a-t" when you read. Rather, you combine those into the single sound "kat" when you read, even though you have done so by looking at the letter symbols. Her omission is important.
She is able to make this omission because we believe we know how to read. Common sense tells us that we're reading the individual letters, even when we're actually reading the word. The letters exist on the page, and each letter has an individual sound; therefore, we must have perceived each one, and that must be how we made sense of the word. Gorman doesn't need to tell us that we've heard the "cat" word as a holistic unit, because obviously we've constructed it from the phoneme sounds. Makes sense, right? Not to Sean Slattery. He looks at a shorter word-- a word whose meaning exists in only one syllable-- and his mind doesn't compile the phonemes. He might hear the phonemes, but his comprehension stops there. He can't hear the word. To hear words, he needs more clues; he needs more context.
Some words are easier for Sean to figure out than others. "I can get longer words, like electricity," he says. "But I have trouble with shorter words, like four or year."
The common-sense linguistic expectation-- that you automatically hear one sound for each symbol and put them together-- evaporates when it comes to music. Gorow would insist that the pitches in a chord are irrelevant if you know the chord as a unit. In traditional musical instruction, I've also encountered the assertion that you don't need to be able to read music at all in order to be proficient. Gorow's book is titled Hearing and Writing Music-- not Hearing, Reading, and Writing Music. I've heard it many times: "music is a hearing art". You hear music, and you transcribe music, but reading it often only gets in the way of its true expression. You can improvise and compose perfectly good music naturally, without reference to written material; therefore the written material is unnecessary. But by the same argument, you'd never need to learn to read or write your own language. You can hear and transcribe language without reading it-- I have been doing just this with Taneda's book, since I don't speak German. You improvise and compose language, without written reference, every time you open your mouth to speak. You don't need reading and writing to have linguistic competence-- nor do you need reading and writing to have musical competence. But in music, unlike language, many people assume you don't need to learn to read.
But what needs to be learned? How does the brain accomplish the reading task?
Researchers have long been aware that the two halves, or hemispheres, of the brain tend to specialize in different tasks. Although the division of labor is not absolute, the left side is particularly adept at processing language while the right is more attuned to analyzing spatial cues.
Amazingly, this is the first time that I've heard the two halves of the brain described this way. I've known that the left side is the language side, of course, but the right side has always been labeled the "creative" or "artistic" side. I hadn't, until now, heard that the right side "analyzes spatial cues". In our culture, where music is learned exclusively as a combination of implied movement and distance, of course music would be processed by the side which analyzes movement in space!
This makes me wonder about the brain scans that have been gathered from people doing musical listening-discrimination tasks. In people with perfect pitch, the note-naming task makes the left (language) side of their brain light up-- specifically, the left planum temporale. But what happens to the right side of their brain? Nothing? Do they fail to analyze the spatial cues which cause someone with traditional perception to hear distance? Does this explain the inability to hear the emotional lift of an ascending scale, because spatial cues and creative-emotion work together on the right side of the brain? And what about listening harmonically instead of as distance-- does that show up on the right or the left side? Plenty of brain scans have been done to analyze what happens in the perfect pitch brain; I wonder if any have been done to analyze what doesn't happen. Gorman describes what the scans have revealed about the brain's structure:
[Functional magnetic resonance imaging] allows researchers to see which parts of the brain are getting the most blood-- and hence are the most active-- at any given point in time. ...Neuroscientists have used fMRI to identify three areas of the left side of the brain that play key roles in reading. ...the "phoneme producer," the "word analyzer" and the "automatic detector." ...The first of these helps a person say things-- silently or out loud... The second analyzes words more thoroughly, pulling them apart into their constituent syllables and phonemes and linking the letters to their sounds. As readers become skilled... the automatic detector becomes more active. Its function is to build a permanent repertoire that enables readers to recognize familiar words on sight. As readers progress... the automatic detector begins to dominate.
For children with dyslexia... Brain scans suggest that a glitch in their brain prevents them from easily gaining access to the word analyzer and the automatic detector. In the past year, several fMRI studies have shown that dyslexics tend to compensate for the problem by overactivating the phoneme producer.
Reading this, all I could think of was Miyazaki's conclusion: "absolute pitch listeners are weak in relative-pitch processing and show a tendency to rely on absolute pitch in relative-pitch tasks." Just like the dyslexics, a person with perfect pitch can recognize all the pitches easily enough, but their strategies for combining those pitches into musical concepts are often mechanical rather than holistic. They need to develop their relative pitch in order to use their "word analyzer", and especially their "automatic detector", in music. This seems to echo a description by IronMan Mike-- who has perfect pitch but claims not to understand how to listen relatively-- of how he transposes an interval. He says he doesn't play "the same interval" in a different place. Rather, he identifies the notes of an interval, shifts the notes, and translates them into the new interval. He does it so quickly that it resembles strong relative pitch, but it's taken him decades to refine this process. Mike's ability sounds like it could indeed be "overactivating the phoneme producer".
The brain's three-piece language processor reinforces my conviction that the separation between absolute and relative pitch is an unnecessary sham. I suggested this week that people who have relative pitch, but not perfect pitch, are musically illiterate; this Time article makes me think that people who have perfect pitch, but not relative pitch, are musically dyslexic.
It may not be an exact parallel, but the processes certainly seem darn close. Levitin has quoted a person with perfect pitch saying "I don't hear the music, I just see pitch names passing by," a situation which certainly resembles a failed word analyzer. I discovered a long time ago that when I am typing in any language, I work the fastest when I ignore the combined sounds of what I am typing and just let the letters pass by one at a time. That way I type more quickly, more fluidly, and more accurately-- but I haven't the slightest idea what it is I'm typing. Then, when I look back on what I've typed, it's as though I'm seeing it for the first time. Gorman's article also describes a person who has no comprehension of what she's spelling.
Imagine having to deal with each word you see as if you had never come across it before, and you will start to get the idea. That's exactly what Abbe Winn of Atlanta realized her daughter Kate, now 9, was doing in kindergarten. "I noticed that when her teacher sent home a list of spelling words, she had a real hard time," Abbe says. "We'd get to the word the and come back five minutes later, and she had no idea what it was."
The critical feature of dyslexia seems to be that people who have it are able to "name" and "recall" phonemes perfectly well, but are unable to accurately combine the phonemes into complex sounds and phrases. Their reading comprehension stops at "phonemic awareness", #1 on the list. And that's the kind of perception I was trying to find, and trying to learn how to overcome. I wanted to know, how do you teach someone who has learned all 12 (phonemic) pitches, but can't recognize them in music? In dyslexia education, I probably have my answer. From Gorman's description, the full dyslexia curriculum seems to directly represent the first five levels of phonemic awareness.
...the most successful programs emphasize the same core elements: practice manipulating phonemes, building vocabulary, increasing comprehension and improving the fluency of reading... the Schenck School in Atlanta specializes in teaching dyslexic students... "Here we have to teach them to recognize sounds, then syllables, then words and sentences. There's lots of practice and repetition."
And, yet, even with lots of practice and repetition, the emphasis is ultimately on comprehension rather than memory. Memory, in fact, is considered detrimental to the process.
How do you know someone has dyslexia before he or she has learned to read? Certain behaviors-- like trouble rhyming words-- are good clues that something is amiss. Later you may notice that your child is memorizing books rather than reading them. A kindergarten teacher's observation that reading isn't clicking with your son or daughter should be a call to action.
(I find it interesting that memorizing a book is considered a call for interventionary action, but that plenty of music instructors at all levels will encourage their charges to "memorize" their musical pieces.)
That doesn't mean older folks need despair. Shaywitz's brain scans of adult dyslexics suggest that they can compensate by tapping into the processing power on their brain's right side. Just don't expect what works for young children to work for adults. "If you're 18 and you're about to graduate and you don't have phonemic awareness, that may not be your top priority," says Chris Schnieders, director of teacher training at the Frostig Center in Pasadena, Calif. "It's a little bit late to start 'Buh is for baby' at that point."
And this ties right back into Mon's experience in learning his phonemic pitches. Is it too late to start "Buh is for baby" at 18 or older? Mon may have tapped into his right-brain "processing power" when he bombarded each pitch with relative affectations-- arpeggios, velocities, key changes, et cetera-- and seems to have accomplished the learning goal. Has he effectively skipped the "buh is for baby" stage, or will he have to eventually get back to it? If not, how important is it, then, to be able to play notes and name them? Taneda's work is explicitly designed for young children. How effective is the strategy of note listening and naming for adults?
I'm reminded of something my mother told me. She's an expert in adult language acquisition, and has developed internationally-acclaimed methods of teaching second languages. When I described the perfect-pitch note-naming exercises, and told her my progress in using them, she nodded and said yes, those exercises would work-- but for an adult, they might not be the most efficient way to learn. Adults learn by association, not by rote. For that reason, she agreed that the trigger words and vowel sounds were a step in the right direction, and I may retain those as I work towards version 3.0 of the Ear Training Companion. I've said that current perfect pitch education is deficient, but I wasn't quite sure how to explain it; now I think I know how (that is, if I have successfully explained it in this entry) and I believe I have a good idea of how to overcome that deficiency.
I'm fascinated that "Dyslexia can be eliminated by education" is important enough, in 2003, to warrant the cover of Time magazine-- yet, admittedly, proof that "perfect pitch can be learned" would be of comparable significance. Although I know that "music cognition" was only identified as a field in 1983, and my best resources (like Thinking in Sound and Harmonic Experience) aren't even ten years old, it still amazes me that these conclusions about the psychology of sound have stayed hidden for so long. I wonder what the field will be like ten years from now?
A few people have wrote to me to point out this news item, and I'd encourage you to check it out.
Origins of Music May Lie in Speech
It can't be much longer now before the perfect pitch myth is exploded. There are too many minds working in this direction for it to persist much longer.