Comments Archive - Phase 8a

I may have been giving pitch-melody association less credit than it deserves. Subject T from Mark Rush's study said that "relating notes to songs... was very helpful." I've heard various voices in the Prolobe forums supporting the strategy, and I've seen it recommended elsewhere, but in each case, I've remained skeptical. Scientific studies have demonstrated that memory for the first note of a song is imprecise, and even though I have discovered from my own experience that it is possible to correctly identify a starting pitch if you remember the key feeling of the melody-- I just this moment recalled a G by whistling the melody of "Lightly Row", and the piano tells me I'm right-- that process seemed far too slow to be of much use. But there is a different use for the melody.

In a role I'm currently playing, I speak German words which include the letters ö and ä. These sounds are not written in the script; this omission drew the ire of one of my professors, and last week we sat down together so he could tell me how to pronounce the words properly. Since I can usually pick up an entire new dialect in a day or two, I certainly didn't expect any difficulty with a couple of mispronounced words.

But I hadn't counted on the fact that the ö and ä sounds do not exist in English. The ä seemed simple; "in this word, you pronounce it like a short e," he told me, and he shrugged approvingly each time I said the word that contained the ä. He then pronounced the ö for me, and I accurately said it back to him. However, after going over a few of the other lines, I tried the ö sound again, and I had it wrong. I wasn't immediately concerned, figuring that I simply needed to repeat it a few times. When I attempted the ö again, he affirmed I was speaking it correctly-- but I was startled to recognize that both times, until he told me, I didn't know whether or not I had it right. With growing concern, I tried again. And again. And I still couldn't tell. Sometimes I said it accurately, sometimes I didn't, and he corrected or confirmed each of my attempts, but in every instance I didn't know if I was speaking the right sound. I even tried repeating the sound without talking in between, but when I did I wasn't sure whether my vocal shape had slipped between attempts!

Both of us were surprised at this difficulty. He was baffled that I kept complaining that I didn't know what I was doing when I was obviously saying it correctly. I was amazed to learn that my mind had no cognitive identity for ö. I could intuitively form my mouth into a shape which, when I spoke through it, matched the sound which I heard from my instructor; but as soon as his model was gone, I was lost. What was going on? I could hear it perfectly well; I could reproduce it exactly; what was wrong? It was like there was an empty space in my mind: where I normally would link the physical shape of my mouth to the aural shape in my head, the physical shape of my mouth reached into my mind and found nothing at all to connect to.

Our meeting became focused on this sound alone. After many fruitless repetitions, I finally began to listen closely to the sound instead of just repeating it. Suddenly something popped out at me. "Oh! It's like the oo in hoof," I exclaimed, "but with this thing wrapped around it!" Immediately, I was able to conceive of the ö as "hoof-plus-wrap", and I confidently concluded our session. As I walked away, I considered what I've been told about how an adult learns-- because of the brain's lack of plasticity, adults learn by association, not by rote. I had the devil's own time trying to figure out ö all by itself, but as soon as I was able to associate it with hoof, the learning was almost instantaneous.

As I continued to practice, however, I discovered that I still wasn't done with this ö sound. Although I was now able to "check my work" by comparing ö to hoof, every time I wanted to speak the ö I found that I had to start from hoof and "wrap" it. My brain still had not given ö its own identity. The empty space in my mind was still empty, and persistently remained so no matter how may times I repeated ö, ö, ö. However, as I started repeating words which contained that sound, I discovered that the shape began to form in my mind. Öffnen, öffnen, öffnen. It wasn't just saying the word, though-- I had to start with the ö. Each time I tried saying "öffnen" without first thinking "ö", I reverted to the English o-as-in-open. I also used the familiar French word "l'oeuf", which is the same vowel. L'oeuf, l'oeuf, l'oeuf. If the ö wasn't formed correctly, then the entire word sounded peculiar. The moment I spoke the word, I knew whether it was right or wrong. By the end of that evening, I had the ö nailed.

The next day, I realized that Dr Remshardt had told me that the ä was like a short e, not that it was a short e. I consulted him that afternoon, and sure enough, he told me that in the middle of a word it sounded like "eh", but it was actually "ä". I repeated ä a few times from his model; as I did so, it became clear that ä was a neutral English a with the same "wrapping" as the ö. Eleanor Gibson was right about perceptual learning through differentiation-- by comparing all five sounds to each other (ö, ä, "eh", "hoof", and the neutral a), my mind automatically abstracted the "wrap", which I assume must be the umlaut, and this made it possible for me to form the ä sound as "a-plus-wrap" (and I'll bet I could pronounce ü correctly if only I knew what neutral English vowel to wrap it around). I was fascinated to discover that in each of the words that had an ä, I heard the "eh" sound as I spoke them-- but my mind thought and my mouth felt a completely different vowel. [Update: the wrapped vowel for ü is "oo" as in pool.]

If this experience is any indication, then melody association is not merely helpful for learning pitches, it's essential. Context is necessary. I learned ö as "hoof-plus-wrap" and then used "öffnen" and "l'oeuf" to solidify its identity; this sounds like what Subject T did, learning "G" as "C-plus-five" and then using Beethoven's 5th to solidify its identity. Because using different words made me learn ö and ä more quickly, I suspect it would be helpful to use additional melodies and chords which also contain G pitches in various places. In fact, this reminds me of some of the levels of phonemic awareness that I wrote about in Phase 7:

It's necessary to choose practice words that begin with the sound. I still can't recall an ä all by itself, because I have been speaking only words that have an ä in the middle, not at the beginning. I know that I'm speaking the ä correctly because, if I weren't, the words would feel wrong; but as a medial sound it remains indistinct. It seems that I need practice in plucking an ä out of thin air, to begin a word, before it will stand on its own. In this same way, I'd expect that a melody that begins with a certain pitch will help your mind to develop that pitch's unique identity. But this process is not simply finding a song and memorizing its first pitch. You need a phonemic mental model of the pitch first. The melody reinforces the pitch, but doesn't create it.

November 17 - Rhyme for a change

Now that I'm nearing the end of Gibson's book, I may put my active research on hold temporarily while I work on the next version of the Ear Training Companion. I began reading Perceptual and Associative Learning, and even though there are some worthwhile chapters on which will expand my understanding of the habituation effect (which Gibson refers to as a reduction of irrelevant information), this book begins by kowtowing to Gibson's work, saying "It is possible that these new mechanisms [of Gibson's differentiation theory] might turn out to be powerful enough to supplant associationism altogether." So I feel adequately confident in moving ahead with what I've learned.

I find myself wondering how much of Taneda's work will prove useful. I'm pleased to discover that the psychology of perceptual learning essentially does not change as we grow up. In fact, adults get better at it. So his principles could be applicable. However, the reason adults improve is that we get better at ignoring irrelevant information-- and we're fighting against years of conditioning that "pitch is irrelevant" (a la Ron Gorow). A critical feature of Taneda's work is that of using colored piano notation, so that each printed note has a unique color (C is red, for example); Gibson has demonstrated that this probably would not work for adults. Gibson conducted an experiment on children, in which she showed them printed symbols ("graphemes"), and asked the children to learn an arbitrary letter name for each. She did not tell them that the symbols were also color-coded. After some training, the children were shown uncolored (black) versions of the same symbols, and asked to identify them. Gibson found that

Taneda says that five years is already pushing the limit for being too old for his method, and this experiment suggests why; Taneda relies on incidental learning. In his method, each pitch sound is persistently and consistently presented in conjunction with a specific color-- thusly, the child develops a unique psychological identity for each note without ever actually being taught that "this is a C" (or whatever pitch). But by nine years old, Taneda's colored notes become ineffective; our minds are too skilled at ignoring extra information.

Nonetheless, thanks to my experience with the German vowels, I am convinced that Taneda's "levels of absolute pitch" is the best conceptual model, and I expect that his work will be a useful resource. Taneda says that the first level is that of being able to identify a single pitch absolutely, from which we expand our perception. As I mentioned in my previous entry, since I knew an ou sound "absolutely", I was able to very easily expand my perception to the ö, which was the "wrapped" version of the vowel, and then create a new psychological category for that new sound. The same should be applicable to pitch sounds.

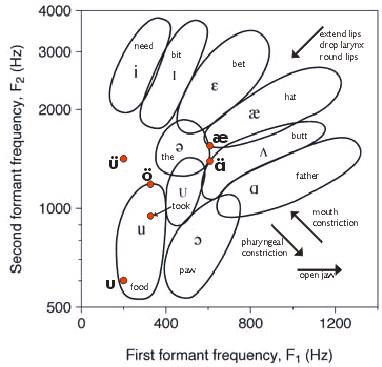
Over the past week, I became curious about the "wrapping" that I had applied to each of the German vowels. I found out that the ü was, as I had suspected, an English vowel that had the same "wrap" around it-- the vowel is oo as in food-- so what was this wrapping? I ran my vowels through a spectrographic analysis to find out. As it turned out, the "wrap" was, in each case, altering the F2 formant frequency while keeping F1 constant. A quick search showed me that I was definitely pronouncing the German vowels correctly, since the frequencies I was measuring in my own voice closely matched another speaker's frequencies. I plotted the vowels on the chart.

Vowel	F1	F2
oo as in food	200	600
ü	200	1500
oo as in hoof	300	900
ö	300	1350
a as in hat	650	1750
ä	650	1400

I was mildly annoyed that my oo-as-in-hoof fell outside the chart's range for the vowel, but a search reassured me that these ranges are typical, not canonical. This chart shows the absolute frequency ranges for vowels, when in fact the vowels are recognized by the relative frequency ratios, not the absolute positions. If that's so, though, then I wonder if what I've experienced with these vowels is a sample of what it's like to hear in absolute pitch.

Having plotted the vowels, I was intrigued that the "wrap" for each vowel meant bringing F2 into the same range (1300-1500), and I gazed at this plot to see if there seemed to be anything interesting about that horizontal band. As I looked, something seemed oddly familiar about the graphic... and then I realized that the red dots reminded me of musical notes. Of course! Since each vowel is a harmonic interval, speaking a vowel "with wrapping" is the same as playing two intervals that share a bottom note (F1) but change top notes (F2). So I converted my sounds to their approximate pitch equivalents.

Vowel	F1	F2	interval (octave reduced)
oo as in food	G3	D5	perfect fifth
ü	G3	F#6	major seventh
oo as in hoof	D4	A5	perfect fifth
ö	D4	F6	minor third
a as in hat	E5	A6	perfect fourth
ä	E5	F6	minor second

Once I'd made this table I saw that, when I say hoof and slide it into an ö, I must be hearing a perfect fifth (A5 to F6). Melodically, my voice has produced a perfect fifth. F2 has, undeniably, gone up five scale degrees; I can see the proof right there on the screen. But I don't hear any musical-type "distance" when I hear my voice speak these harmonic intervals. Not at all. I don't hear a single bottom note with a top note that "moves". I hear two different vowels, one following the other, separately. My mind takes each pair of top and bottom notes together, and they are unrelated to the next pair. I recognize and perceive vowel "intervals" from their qualitative differences alone, with no sense of distance. This allows me to perceive language as a succession of harmonic states. That's what WA Mathieu was talking about, and it seems very likely to me that this could be why Mike has said, more than once, that he perceives intervals and music without any need for "distance" or ordinary relative pitch. If so, then this lack of distance perception that I hear when I speak these vowels could be identical to a person listening to music absolutely.

With this further evidence that language and absolute listening are linked, I contemplated the primary levels of phonemic awareness, thinking that they would have to be addressed by a new curriculum:

I puzzled over level two for much of this past week. The first level didn't seem daunting; Taneda starts his training with chord recognition, and I figured that simple music theory can demonstrate to an adult listener that a piece of music can be broken down into measures, progressions, and chords. But how does music rhyme? "Bat" rhymes with "cat", and they each have three phonemes; does a I chord "rhyme" with a V chord because they share the same root? Or is that more like alliteration? And what about chords that aren't triads, or rhyming words like "fuss" and "gregarious" which have different syllable counts? Maybe this is the difference between a chord and a two-note interval...? What could it be?

I finally put the question to our show's accompanist (she has perfect pitch). She reflected a moment, then gave me her answer: to her, rhyming structures are musical phrases that end on the same chord. As I thought about this, I felt somewhat foolish for not realizing this myself-- in a pair of rhyming words, it is the terminal syllable, not the last vowel sound, that matches. Since I consider a word to be parallel to a musical phrase, and a chord to a syllable, of course a "rhyming word" is a phrase with the same chord at the end! Duh. I'm pleased to have this answer, though, especially since she gave it to me without my having to explain what I meant; all I asked was "what 'rhymes' in music?" and this was her immediate response. I'm encouraged to think that each of the levels of phonemic awareness can thus be represented-- and, presumably, taught-- in musical sound.

November 22 - Hear me, peel me

Over the past few days, I've managed to confirm one of Gibson's findings-- perceptual learning occurs, whether or not you're trying.

I discovered this almost by accident, since I merely wanted to test one of the exercises in Taneda's book. Taneda's method is designed to teach very young children, but there are some aspects of his work which don't seem age-specific. One of his exercises, for example, involves listening to and identifying the C-major I, IV, and V chords, alternated with meaningless clusters. I didn't see why an adult couldn't do this-- in fact, I thought it could be too easy for an adult-- so I programmed the exercise into the computer. I made the computer play the I and IV chords (C-E-G and C-F-A) automatically while I sat back and listened. I very quickly discovered, at least superficially, that Gibson was correct that there's no need be told whether or not I "got it right"; if I identified one major chord wrongly, I knew my mistake as soon as I heard the other major chord. Discovering a correct answer on my own is much more satisfying than being chastised for a wrong answer by someone else (even a computer).

On the second day of listening to the chords (the first session had been 20 minutes), I was surprised when one particular pitch sound started to jump out at me. I hadn't been trying to pull pitches out of the chords; I had, in fact, been trying to hear them as unified harmonic events. So it was strange that a pitch sound had decided to peel itself away. I listened curiously to the pitch sound a few times as the exercise continued, but didn't attempt to identify the pitch. If Gibson is right, I contemplated, then my mind would have recognized the I-IV chords as the transformation of a single chord object, and been unconsciously looking for the invariant sensation within that transformation. Therefore, since the I and IV chords share only the C, this pitch I'm hearing is probably a C. I stopped the exercise and identified the stray pitch-- first in my head, and then on the piano (to be doubly certain). Indeed, it was a C.

In the third session, I found that the other pitches began peeling themselves away from the chords... and they seemed to be sounds I heard in addition to, not instead of, the entire harmonic sound of the chord. I wasn't actively looking for them, I didn't try to hear them; they just presented themselves to me because I was casually listening to the different chords. Am I also unwittingly gaining a feeling of "C-major" by doing this exercise, as Taneda intends, by listening to the C-major chords versus random clusters? It certainly seems possible.

Since I've railed so frequently and so consistently against note-naming, I considered the fact that this exercise was chord-naming. "Identification leads to generalization", says Gibson, "which is the opposite of perceptual learning." By identifying the chords, was I somehow working against perception? But I concluded that a chord is an object, not a sensory percept. Gibson acknowledges that categorical practice can lead to the discovery of higher-order features, like relationships, and a chord is definitely a collection of pitch relationships. So chord-naming is perfectly fine, and theoretically productive.

I'm encouraged-- not just by the actual effect of this particular exercise, which has been fun, but because its effect makes me confident that I can develop exercises based on the theoretical assumption that invariants will be extracted whether or not we're actually trying to find them.

December 7 - And now a word

I'd encourage you to take a look at this illuminating retort by Iron Man Mike in the Yahoo discussion group. His lengthy statement is a rational rebuttal to the increasingly petulant assertion that "without relative pitch, music is meaningless; therefore people with perfect pitch must hear in relative pitch, even if they aren't aware of it."

The more I learn about musical perception, the less meaningful it seems to try to categorically separate "perfect pitch" and "relative pitch". To begin with, I've recently met people whose perception fails to fit neatly into either group-- in fact, one of these people would require a third category. In addition, the simplest examples of phonemic and syllabic comprehension should make it intuitively obvious that single sounds and sound combinations are interdependent, although I have more sophisticated evidence besides (and plenty of it). I'm pleased to reference Mike's post as the proverbial icing on that cake.

December 17 - Pulled up by the roots

Thanks to a little more feedback, especially from Alain, I've finished the Chordsweeper game (although additional suggestions are always welcomed). I'm still not done with ETC v3.0-- Chordsweeper is just one component of that, but it's still fun to play by itself.

Now that I've been playing Chordsweeper for a little while, I'm pleased that it seems to be accomplishing both of the goals which I theorized it would. I expected that listening to two different chords that shared one similar pitch would cause that "invariant" pitch to become more prominent, and that does happen. "The root just seems louder," according to a couple beta-testers, and I've heard this myself too. The other effect that I'd hoped for was that, by playing the I, IV, and V chords in different keys, the player would begin to get a feeling for each key. Even though I'm only on Level Two of the program, it seems that I'm beginning to recognize when a tone belongs to the "dog group" or to the "cat group". As I continue to advance, and more key sounds are introduced, I'll find out if this is really what's happening.

One thing I can't quite explain is that, when I hear a V chord (the brown animals), I don't hear the pitches simultaneously. In fact, I have learned to recognize the V chord by listening for the "da-dum" of the re-ti sequence. The other chords don't do this. I thought maybe it was something wrong with the way Chordsweeper was playing the notes, but I went to my piano keyboard, played the V chord, and I still heard the da-dum.

Well, actually, I can explain how this is possible. It is probably the same psychological ability which makes the syllable "tap" sound like a T followed by an A followed by a P, even though the sounds occur simultaneously. What I can't explain yet is why my mind decided to interpret the V chord this way, as asynchronous pitches. It must have to do with the fact that V shares one pitch with I (sol), so my mind is picking out the two pitches that are different... but when I hear IV, which also shares a single pitch with I (do), I don't hear the fa and la separately! I suppose I'll just have to keep listening and see what happens next.

December 21 - The child is father to the man

Jenny Saffran's research has propagated the idea that everyone is born with perfect pitch, but loses the ability as they grow up. This is such an appealing idea that it's already being spoken as fact in various corners, and a quick look at the surface seems to be in agreement. It is true that Saffran's conclusion seems to be supported by genetic theories such as Jane Gitschier's, which claim that people with a perfect-pitch gene must be exposed to relevant learning, in order to "activate" the gene, or they lose the potential. Saffran's conclusion also seems to be supported by the infant research from The Scientist in the Crib, which demonstrated how children gradually unlearn precise phoneme distinctions which are not reinforced by their native language. I'd synthesized this information into my own conclusion: that nobody is "born with" any specific ability to interpret sound, but gradually learns to interpret what they are hearing based on elements of nature (an enlarged left planum temporale, perhaps) and nurture (early musicianship, or being exposed to tonal music).

A few days ago I was casually reading the final chapter of Thinking In Sound, "Listening Strategies in Infancy", by Dr Laurel Trainor and Dr Sandra Trehub. It started to challenge my "born with" conclusion, using this point:

It took me a little while to figure this out-- partly because it's a grammatically circular statement, but also because there's a hidden assumption which I had not considered: human minds "want to" make sense of the world around them. The mere act of listening is a learning experience. That means our minds must have some innate strategy which will be applied, or else no learning would take place at all! The article grabbed my full attention as I read:

I must have been wrong that we are "born with nothing". We must be born with some kind of preferred strategy for interpreting musical (tonal) melody. And these authors' experiments promised to tell me what that strategy is.

Babies can't talk; how can we know what they're hearing? Well, when an infant hears a new sound, it pays attention; when the same sound is repeated, it loses interest. This response is both "unambiguous" and "reliable". This response is what the scientists tested, and it is from this response they generated their results. This response, it must be acknowledged, is a simple yes/no judgment. Babies cannot give qualitative answers, nor can they describe their experience. The researcher can test whether or not the infant thinks that a new sound is "same" or "different" than what came before-- and that's all. The value of the experiment lies in the researcher's ability to ask the right questions. And this article seemed to be asking good questions.

Trainor and Trehub figured out that among contour, interval, and pitch information, the babies chose to interpret music using contour. Overwhelmingly, consistently, contour. The researchers learned that the babies listened with "...information about pitch contour dominating at the expense of absolute pitch and interval information."

Here's a highly simplified summary of what the researchers did, starting with a typical sample melody. The line I've drawn beneath each staff represents the "contour" of the six-note melody (the up/down/same pattern of the notes).

In order to understand a baby's recognition of the changes, the scientists designed different series of repetitions, to systematically isolate each type of change (contour, interval, pitch) and thus determine how the babies responded to each type specifically. They conducted multiple experiments with all kinds of variations, to cover all the possibilities. Here's one example.

If you agree that, overall, the researchers did succeed in isolating each type of change, and that their methods were adequately conclusive in determining that babies respond to contour, not intervals or pitches-- what about Jenny Saffran? What does this say about her suggestion that all babies have absolute pitch?

I don't (yet) have Saffran's full article, but I have one comment about its press release: there appears to be no mention of "contour" whatsoever. If contour is a demonstrable musical identity, and Saffran has omitted any test of contour, then her research is necessarily incomplete, and consequently it is inconclusive. "Saffran's lab developed a test to manipulate the pitches of songs to determine whether her learners were following absolute or relative pitch," says the release. That's "relative pitch" (intervals) and "absolute pitch" (pitches). Nothing about contour. If Saffran failed to vary the intervals in her transposed melodies, then there's no way of knowing: were the adults truly following the intervals, or were they just skimming the contour? Of course, this particular oversight needn't directly oppose the babies' responses, but could reveal a conceptual flaw in her model. I have other questions about Saffran's methods, too. How does she know that babies can understand a three-minute melody? And, since they had heard a three-minute melody, why would they respond to a short segment as though it were the same? Is it possible that the "absolute pitch" which she says they detected somehow altered the contour? Is it a fair assumption that detecting the absolute pitch of a melody fragment as "different" means that the baby actually recognized a pitch? After all, it's been proven that even the tone-deaf can detect key changes. And were the adults asked "Is this the same song?" or asked "Does this sound different?", each of which an adult might answer differently? ...These questions (and others) will have to wait until I see her article, and I do want to find that article and see how her data compares to these researchers', but I now find myself extremely skeptical of her conclusion.

My skepticism isn't based on Saffran's experiment alone. At the very least, if you accept that hearing exists to detect motion, and that we listen to music as though it were an invisible moving object, then it becomes patently obvious that the same movement (contour) is going to seem the same. Six inches up is almost the same as seven inches up, but it's clearly not six inches down!

Furthermore, I've met people here at school who are direct evidence of what Trainor and Trehub found. The researchers wondered-- do we have some inborn strategy for processing music, which simply stays with us if we don't get any specialized training? If so, does exposure to tonal music reinforce those natural abilities? They asked the question this way:

If my classmates are any indication, the answer is a resounding yes! As I've observed my two non-musical classmates' attempts to sing, they've done exactly what these researchers discovered. My classmates use contour "at the expense of" interval or pitch. (The class, by the way, was "Fundamentals of Musical Theater"-- a simple exploration of basic song, dance, and musical expression, open to all majors regardless of musical talent.)

One girl had to sing "Another Suitcase In Another Hall" from Evita. She doesn't read a note of music (sheet music is a complete mystery to her) so one day, as she practiced a cappella, she asked me to tell her whether or not she was singing it correctly. I found her starting pitch for her, on the piano, and she began. She sang the first phrase correctly, except that it ended on a large upward interval for which she jumped too high. But then, by singing properly the intervals that followed, she immediately modulated into the correct key for the higher note. Amusingly, she did the same thing on the return trip; she sang a large downward interval too low, and then instantly changed keys to accommodate the "mistake". Once she was done, I told her that she'd changed keys a few times-- but she told me she hadn't noticed. Very likely this was because the contour was the same, even though the intervals and pitches were different.

It occurred to me that her demonstration supports what Terhardt was saying. Tonight in the car I was listening to Keith's "Ain't Gonna Lie" and, at the end of the song, it modulated into a different key-- by doing exactly what she had done. When there was a large upward interval, the singer took the interval "too high", and then immediately produced the correct intervals afterward to modulate into the new key. In that critical moment of change, the contour remains the same; therefore, even though the interval and the pitch are different, the listener is willing to accept in that moment that they are hearing the "same song". The similarity is then quickly reinforced by the subsequent appearance of identical intervals (and contour). (How funny-- I only just now did a Google search for that link to Keith, and I'm delighted to find that there's an MP3 of "Ain't Gonna Lie" right there that you can download and listen to! It's only 96kbs, but that's still a better quality than the scratchy 45 I originally converted mine from. The downloadable version of "98.6" is some kind of alternate take, though, rather than the actual hit version... that's probably a rights issue.)

The other fellow's situation was a bit more complex. Whereas (once you added the piano for reference) the "Suitcase" girl sang quite beautifully, this guy was certifiably tone-deaf. Recognizing this, the instructor had assigned him "Greased Lightning", which has small intervals and is more of a patter than a song; but he still couldn't do it, even when the accompanist played nothing but the melody. I didn't really bother to wonder why until I heard him make one particular attempt. After he sang the chorus correctly, the next verse began with a higher pitch, which he sang painfully flat. But then he sang the rest of the verse equally flat. Every note was just as flat as all the others. He didn't modulate, or self-correct to the piano, so it sounded horrible-- but all of his intervals were accurate. Perhaps, like the "Suitcase" girl, he was simply unable to judge larger intervals? I resolved to ask him about this after class.

When I approached him, I asked, "If you were to physicalize your attempt to hit that interval, how would you do that? Would you stretch your arms to reach for it, or jump up towards it, or look up at it, or..." He cut me off to say, with some confusion, that it wasn't any of these, and in fact wasn't even anything like what I was suggesting. "It's like each note has a certain energy," he explained, "and when I sing a note, I try to give it that much energy." He went on to explain that he didn't feel the notes' relationships to each other at all; he would sing what he thought was the melody, and if the instructor told him that he wasn't doing it correctly, he would have to try to pay attention to each note individually. "And that's so slow!" he moaned. "I can't do that and still follow [our accompanist]."

This made me think about the people with absolute pitch who complain that music is just "pitch names passing by." Was this guy naturally tending towards absolute pitch? If he has no sense of the intervals, and produces a melody as a series of pitches, perhaps he recognizes music with a form of absolute listening! I mused happily about this possibility until I read the article in Thinking in Sound, which made me realize what I'd overlooked. Even without paying attention to pitches or intervals, he was singing something that his mind told him was "the melody", and that something was consistent and accurate even when it was "flat". That something is very probably the contour of the sound. During that time when he was flat for the whole verse, he would not have self-corrected, because his mind told him he was still accurately following the piano's contour. Then, when asked to consider the components of the music, his reliance on individual pitch sounds is not necessarily due to a latent sense of absolute pitch, but could be due to lack of structural perception, which would require him to attempt to assemble the melody from its most basic components. Nonetheless, this fellow's experience does provide additional evidence that contour is our "born-with" method of interpreting music; it's only after he's asked to pay attention that he uses the pitches. Contour comes first.

Also, there's one more tidbit to point out: his other natural strategy for interpreting musical segments was to pay attention to the pitches, not the intervals, even though he definitely does not have absolute pitch. Does this have any implication for Saffran's research, in which babies interpreted musical segments using pitch information instead of interval information? Now I really must get hold of her publication!

I also need to mention that all of these experiments-- the ones I've mentioned here, as well as the relevant ones I haven't included-- are exclusively musical. I suspect, considering the evidence I've cited before about illiterates having no phonemic awareness, that similar experiments could be constructed with language sounds to achieve identical results. The authors who conducted these experiments do note the similarity and acknowledge the possibility. In which case, if the primitive processing strategies did prove identical for both, I'd be terribly curious to know when the brain starts feeding "language" sound and "music" sound into its different sides.

Underlying this entry is one main point that I have been contemplating for a while but am now quite certain of-- "relative pitch" and "absolute pitch" are outdated and limiting concepts which are incomplete, misleading, and in Saffran's case damaging. An entire section of "Listening Strategies in Infancy" demonstrates how the consonant structures of Western music-- "relative pitch"-- are actually what makes it possible for an infant to recognize pitch changes. I'm glad to read this, partly because it provides additional theoretical support for Chordsweeper (which now has its own help page, even though it's not officially released, because I've been playing it and I'm kind of addicted to it), but also because it provides some scientific justification that trying to learn "absolute pitch" without any regard for structural concepts-- or, worse, actually suppressing your structural knowledge in the attempt-- is as likely to be successful as attempting to learn letter sounds while ignoring the existence of words.

December 26 - Any way you slice it

This week I've been re-reading How Children Fail by John Holt. I'll be teaching in a couple of weeks, and I wanted to remind myself of strategies which the book illustrates, but I also found something directly relevant to this work. In fact, following directly on the heels of my previous entry, Holt pulls together what I've been saying against existing perfect-pitch training strategies. Before now, here and there, I've been picking and poking to make individual points: why note-naming is counterproductive, why memorization is ineffective, why structural knowledge must not be ignored, et cetera. Because of this, people sometimes ask me, "But how can you learn perfect pitch if you don't study and memorize the pitch sounds themselves, to become familiar with them?" and I haven't had a complete answer to give. Fortunately, Holt, in this lengthy quotation, describes the big picture. Although he's talking about mathematics, the same concepts apply directly to pitch study. For example, you can read the first sentence as "pieces of information like C + G = perfect fifth are not isolated facts," and then consider the rest of the quotation with other musical terms instead of mathematical ones.

What help is it to be able to recognize pitches if that ability bears no relationship to your performance, or to scales and modes, or chords, or... or anything at all? It is pointless to memorize a "C" or an "A" or even the entire piano keyboard if that knowledge has no application and no context; furthermore, if memory fails, you are perfectly capable of saying that an F is a C. But once you understand the tones, their relationships to other pitches, the structures which those form, and their relationships to other structures-- then you can hear pitches, in all their different disguises, without being fooled.

Bolek, in Poland, has kindly provided the "translation" of the above quote into musical terms. Kudos-- and thanks!

January 7 - Bucket of frogs

Here's a simple experiment you can do right now. Pick up a pencil or a Tootsie Pop or something and begin tapping out a steady beat on the desk in front of you. As you tap, think of the taps as single beats: "One... one... one... one..." and so on. Do this for a little while-- and while you listen, notice that the sound is exactly the same each time. Tap, tap, tap. One, one, one. Same, same, same. Then, once you're convinced that it isn't changing, keep tapping in precisely the same way but start thinking "One... two... One... two... One... two..." After a few moments to adjust to the one-two rhythm, listen to each beat. You'll hear that "one" sounds like a higher pitch than "two", even though they're exactly the same sound. If you're feeling adventurous, flip it around so that "one" is now "two" and vice versa, and now the other pitch will sound higher.

I've found that I can reproduce this effect with any steady beat. I initially thought that I could be selectively listening to different harmonic overtones of the percussive signal, or maybe that I was subconsciously allowing myself to tap harder or softer, but I was able to create the same result using a simple sine wave on the computer. If you want, have a friend tap for you, and don't tell them which is supposed to be "one" or "two". So far, everyone I've demonstrated this to has instantly heard the difference.

This helps illustrate at least one aspect of why teaching perfect pitch has always been so elusive-- there are too many influences which our minds are willing to accept as "pitch". All the training methods that I'm aware of (and Mark Rush created a commendably exhaustive list) try to teach "pitch" to their subjects without first establishing an appropriate answer for "what is pitch"? They have many interesting and creative ways of prompting the user to listen to, memorize, or learn "tones"-- but, as this simple experiment (and the rest of my website) will show you, pitch is just one aspect of the tone.

I've got my own answer for "what is pitch", as I've mentioned before: the instantaneous velocity of a physical movement. I've therefore confidently suggested that musical "contour" is our mind being convinced that there's some imaginary invisible thing moving up and down out there, but just this week I considered another potential implication of this definition-- octave equivalency. The purpose of hearing is to detect movement. Our ears are designed to interpret sound logarithmically. Constant acceleration produces a logarithmic pattern. Newton's very first law is that "a body in motion tends to stay in motion"; so that (as the neon sign of any tacky storefront can demonstrate) when our senses are subjected to a progression of stimulus that follows an unchanging pattern we can't help but instinctively apply that law and perceive a single movement. Therefore, as far as our minds are concerned, playing a sequence of octaves-- B1, B2, B3, and so on-- is a single body moving with constant acceleration. According to the way our minds have been designed to interpret the universe, the tones are not two similar sounds, nor two identical pitches, nor even a single object moving from point A to point A', but are in fact a unified temporal representation of a single, fused event. This idea makes me wonder if perhaps this is a natural explanation for why tonal fusion exists.

This is a fairly idle thought, though, since I don't have the slightest bit of proof to back it up nor any particular application to put it to. But between it and the one-two experiment, I've realized that in designing the third component of ETCv3 (the part that will teach perfect pitch directly) I can't just brainstorm different musical contexts in which to present a tone. That is-- Gibson's book says that in order to teach perceptual learning, you need to present the target stimulus across multiple transformations, and I was thinking of those multiple transformations as a generic list of musical structures: chord, arpeggio, scale, etc. But as the lollipop experiment helps to demonstrate, there's more psychology affecting our pitch perception than merely how the pitch appears in some musical structure-- there's rhythm, dynamics, prosody, and implicit movement, for example, at the very least.

January 12 - Errata desirata

I now have a clutch of questions about aural perception that I regularly ask of musicians when I meet them. What I've been surprised to learn is that how they answer the questions-- how they respond to the language of the question-- is usually more important than what they actually say. Typically, if the question is asking about something they normally hear, they'll answer "yes" without hesitation. But if their answer is no, they don't say "no". They look confused and don't understand the question. Why should they understand it, if the question doesn't make sense?

The best example is my favorite question: "Do you hear an emotional lift from an ascending scale, and an emotional drop from the same scale descending?" Anyone with ordinary hearing will take a moment to imagine the notes in their head, then nod and smile and say "yes, I suppose so." Someone with perfect pitch, on the other hand, won't know what you're talking about. If you can manage to explain what you're trying to ask them-- which is not easy-- then they shake their head and say "no, they're just the same notes in reverse order," and probably wonder if you're putting them on. I've also found that a person with perfect pitch may not understand the question "Do you hear distance between notes?"; it took me literally five minutes to explain this question to our accompanist-- a phenomenally talented pianist and a very smart woman-- before she finally decided I was talking about the distance between piano keys. This is the same woman who, when I asked her a question I didn't fully understand ("What two musical structures could be said to 'rhyme'?") answered instantly without any need for further clarification ("two phrases with the same chord at the end"). Any question about musical hearing is naturally biased, and someone who does not have that bias in their own hearing probably won't understand the question until they hear it rephrased in their own terms.

Sometimes, knowing typical biases makes it easy to predict what responses I'll get. In the previous entry, I mentioned that the lollipop illusion was "instantly" recognized by "everyone I've demonstrated this to", but none of those people were musicians. I expected that someone with perfect pitch, or someone with a strong sense of pitch, would probably have to work to experience the same effect, if they could even hear it at all. [The small flurry of e-mails I received confirmed that point.] In any case, once I know the typical responses for each question, I stay alert for those who answer unpredictably. The ascending/descending question is usually the first clue, and for that I got a couple of unusual answers last month.

One woman readily said that she hears the emotional change-- but in reverse. An ascending scale, to her, represented discomfort and anxiety, and a descending scale meant security and stability. A glance at Emmanual Bigand's "Contributions of Music to Human Auditory Cognition", also from Thinking In Sound, shows that an ascending scale creates an overall "pattern of tension", and a descending scale a "pattern of relaxation", principally caused by the relative consonance and dissonance of the individual notes to the tonic (although there are surely more factors than that). I wondered if perhaps her answer was just a semantic difference. Where I suggest lift she feels agitation, and where I say drop she feels relaxed; those sound almost similar enough to be a simple misunderstanding, except that I (and most ordinary listeners) feel a qualitatively positive "agitation" on the upswing, not a negative one. Does this mean that she experiences musical contour differently? Does she hear pitches moving freely, or is there some kind of tether to the tonic which stretches like a rubber band? Unfortunately, the time it took to establish what we were both describing was all the time we had together, and now I can't ask her any more because I don't know where she's gone.

Fortunately, I did have more time to talk to another woman I met backstage at my last performance. She overheard one of my discussions with the accompanist; with some curiosity, she identified herself to me as a singer (this was somewhat unexpected because she was there as a stagehand, but that seems to be the lot of the undergraduate here) and I soon asked her about how she hears the scale's emotional lift and drop. Her answer was unusual in two respects. Firstly, although she asked me to restate the question, she didn't require any further explanation; secondly, with confidence, she answered no. This was strange-- how could she understand what I was talking about, but still not hear it? Although, in the next moment, we each had to attend to our preshow duties, she approached me during the intermission to say that actually, she does hear an emotional lift or drop-- but only if the scale is played with all twelve tones, instead of just the usual eight. This conversation became the rest of our intermission.

From her, I learned that there is a third general form of musical hearing which is neither "relative pitch" nor "absolute pitch": solfege pitch. She can tell you the absolute scale degree of any tone, without a reference, but couldn't tell you the pitch name. If you play her a musical interval, she'll name it instantly, with no regard for its absolute position-- but if you ask "how far apart are the tones?" she has to start counting, because she doesn't hear distance. She can transpose effortlessly, but when she transposes or harmonizes, the notes she sings do not sit any "distance apart" from the original melody; instead they blend together (with the melody or with each other) to achieve whatever specific harmonic feeling she desires. She is familiar with the general sensation of many key signatures, but not the absolute pitches in which those keys are rooted. She explained that she feels the emotional change from an ascending or descending scale because "when they're ascending, I think of them as sharps, and those key signatures are usually happier; when they're descending, they seem to be flats, and those keys are usually more mellow." She said she doesn't feel, as the rest of us do, an emotional lift (or drop) which continues to increase (or decrease) as the scale continues to climb (or descend)-- rather, each scale creates a single, distinct sensation. ["...and that's mellow, not somber," she insisted.]

As we talked further, it became more and more clear that "solfege pitch" is a complete psychological strategy which deserves a category of its own. Yet the way she hears and responds is a hybrid of relative and absolute effects. From most of what I've read, but especially since that conversation, I tend to think that it is a fallacy to attempt to categorize any listener as having "absolute pitch" or having "relative pitch"; there are many different ways to perceive many different aspects of music, and applying to any person the label of relative, absolute, or even solfege creates a broad, limiting, unhelpful prejudice of what we "know" that person hears.

In other news, Diana Deutsch has a new CD available. The sample tracks, especially Track 22, are delightful. One thing about it surprises me, which is her suggestion about "memory stores" for pitch. Visual, numerical, and logical tasks must use different parts of the brain than does music. I know that I can't listen to music if I want to write or study, but that music does not confuse my ability to draw or design. I didn't know until just last month that I can focus perfectly well on computer programming, never losing my line of logical thinking, and actively enjoy music at the same time. I wonder if Deutsch's results represent a task-interference issue, rather than memory... or if perhaps she would consider that to be the same thing. I don't think it is the same thing, though. Thinking of musical contour makes me wonder if the person making the same/different judgment isn't actually remembering the absolute position of a tone, but instead judging whether or not the tone moves up or down. In that case, you'd get different results depending on your musical approach to the final tone-- but that is task-oriented, not memory-based. (Addendum: I contacted Diana Deutsch about this; she agreed that the situation is not a simple one, and she seems to have thought of this exact question. She offered to send me reprints of her research papers which address the memory question. When they arrive I'll let you know!)

Even if it were memory, I'm not sure I see why it'd be remarkable for numbers not to interfere with music. As I was walking towards one of my classes alongside the head TA, she commented that she is dyslexic-- but only for numbers. She reads and produces written language without any difficulty whatsoever, but when she sees numbers she often transposes digits. As I discussed it with her, it seemed that number-dyslexia is similar to phoneme-dyslexia; their brain grabs the entire word, rather than its components, so that at first glance the number-dyslexic would think the numbers "38925" and "39825" equivalent, because they have the same first and last digits and all the same components. But despite the similarity of the disorder, it evidences a neural distinction between numerical and letter symbols. I'm not sure that it's important to demonstrate that listening to words doesn't prevent you from "remembering" tones; it seems to me like that's the same as saying that carrying a box doesn't prevent you from kicking a ball. You use different parts of yourself-- why would it interfere?

Speaking of ambiguous research, thanks again to the university's resources I did manage to get hold of Jenny Saffran's publication. I thought I'd take issue with the research; instead, I simply disagree with the conclusion. I appreciate that her own words are far less self-congratulatory than the news headlines; where the headlines trumpet "All babies are born with perfect pitch!" she says more cautiously "...these data suggest that at least under certain conditions, infants have access to absolute pitch information and can use absolute pitch cues." Overall, she seems to have demonstrated that adults learn relative pitch, not that infants have absolute pitch. All the same, I can appreciate this experiment-- if she has proven that infants "have access to absolute pitch information" which they are subsequently trained to ignore, then it must logically follow that by applying Taneda's method (or something similar) babies can instead be trained to use that absolute information.

Some things can't be trained at all, though. Some people have no visualization ability whatsoever and could not be trained for it. I found a couple other people who have the same condition, and I thought of them in class the other day when I was asked to close my eyes and visualize things. As the teacher suggested a variety of images, I wondered how many people like them she might have encountered in her career. But after some visualizing, the instructor continued with the other senses: taste, and touch, and sound, and... and then... and then I learned, to my shock and astonishment, that I can't smell anything in my imagination. This isn't just memory; the sense is wholly absent. I tested this at home by sticking my face in a can of coffee grounds, then turning around and immediately trying to reproduce the sensation in my mind. Nothing. I recognize smells when they occur in the world around me, but I can't recreate them in my head. In my mind, I can look at a lemon, feel its heft, examine its texture down to the smallest pore; I can put a segment on my tongue and wince at its tartness. But I can't smell it-- not even if I shove an imaginary piece directly up my imaginary nose. By extension, if there are people who can't visualize things and people like me who can't... olfactorize?... smells, then there must be, somewhere, people who can't auralize sounds.

We can train completely abstract concepts into our mind. On three separate occasions in the past few months I've poured out (into different containers) what I've judged to be two cups of water; and then, transferring the water to a measuring pitcher, discovered that not only was I correct but I was precisely correct. This is very probably the same kind of learning as when we learn to conceive other abstract features of an object like weight and length and size-- or, in the case of musical structures, distance. I still haven't found a conclusive argument about whether there really is any value in learning to hear "distance" in music-- Ron Gorow swears by it exclusively, and Bruce Arnold condemns it unequivocally, but the solfege listener still has to laboriously count when she wants to know how far apart two notes are placed. I posed the question some while ago, and suggested that this is how you find the notes on your instrument when you play; but the half-keyboard research shows the information is mapped to a finger, not to a spatial position. Ron Gorow says that being able to use distance is critical for transcribing regardless of the context; but the solfege listener adjusts to the context and doesn't give a whit about distance. Why, then, is there any use for learning to hear notes as "distance", other than the mere curiosity of being able to do so?

January 19 - Go 'fege

Sébastien has asked a question about the girl who hears in "solfege pitch", and his question may be on others' minds as well: "Can you try to be more precise, I don't understand her case. Especially, to hear a scale degree, you need to have a reference! Don't you?"

I suppose it depends on your definition of "reference". The other week, when I was still practicing "On This Night Of A Thousand Stars" for class, I woke up with the song on my mind. Specifically, I woke up with the first note in my head, and it felt strangely like a mi. I struggled out of bed, grabbed the sheet music, and sure enough, the note was a B in the key of G-major. You can do the same thing for any song you're familiar with; I just this moment considered the first note of "It's Still Rock and Roll to Me", which felt like do, and a glance at the piano book confirmed it (C in C-major). I also suspect that the first note of "This Magic Moment" is a major sixth from the tonic, although I don't have sheet music to be certain. When you identify the first note of a melody like this, there's no "reference" because you don't need to hear any additional notes to recognize the scale degree; however, your mind has to be adjusted to the key feeling of the song. That's a kind of reference, I suppose, although it's entirely internal.

There was one aspect of her musical production which I neglected to mention. Although she can effortlessly sing harmonies, and sight-sing very easily, she reads instrumental music kinesthetically. That is, she associates the printed notes with physical movements. She doesn't let her fingers find sounds she's already hearing in her head. This is the opposite of what absolute listeners report; they typically describe how, like a touch-typist uses a computer keyboard, they hear the sounds in their head and their fingers almost automatically fly to the correct places to produce those tones.

I've been thinking lately about what Taneda had to say about learning to read piano music. A young child is not really learning to read music, he said; rather, "the sounds and movement are flowing from the child’s memory." I wonder if that ever really changes? The solfege girl described how each piece of new music was very tedious to learn; when I mentioned this to my father (a former clarinet player) he concurred that learning each new song was a pain, but "the reward was then being able to play that song." Is this everyone's experience? If so, then, when we learn a song kinesthetically, are we really reading the music when we play it again? I doubt it. It seems more likely that we use the printed music as a reference to impress the movements into our minds and our muscles; then, when we return to the sheet music, we aren't reading the song-- rather, as I put it before, we're "using what [we] do know about musical notation to find visual cues that would allow [us] to access the memory of how to play the song." This is similar to the experience of one of my classmates, who, if he isn't truly dyslexic, has a serious reading disability. If you hand him a piece of text for him to read unprepared, he'll stumble and stutter and fail to make any sense of it-- but if he's given time to "learn" the piece, he can perform it beautifully and powerfully. In one of our classes, we were given a monologue to read at the end of the hour. As I sat next to him, I overheard him quietly, haltingly, speaking the words aloud to himself, trying to remember enough of its structure so that he would be able to "read" it when called on. Is this very different from the musician who has to play the piece in order to know what it sounds like, and who then relies on their physical memory to be able to reproduce the same sounds? It does work, but it's inefficient.

The goal should be to hear the sounds first and find the keys afterward. I'm pleased that Chordsweeper appears to be a step in the right direction. When playing Chordsweeper (I'm up to Level 5, Round 3!), I've discovered that I can often make a good choice by listening to the sound, then pointing at a tile, and letting my body feel whether or not it's the tile I'm looking for. Without any kind of conscious thought, the answer bubbles into my emotional state and I know whether or not to click. Although I can't explain why that should happen-- not yet, anyway-- it seems to be an absolute-listening experience.

February 6 - Learning together, growing together

The show I was in closed last week, and even though I still haven't caught up with everything that was put on hold during its final weeks of rehearsal and performance, I promised to tell you when Dr Diana Deutsch had sent the research she'd promised-- and it arrived today! She included more than a dozen articles, and three book-chapters, on pitch memory and contextual effects. I'm looking forward to reading them; I'm especially intrigued by a 1975 publication, "Disinhibition in pitch memory", which may further inform my previous exploration of absolute pitch perception as a form of reflexive response.

I received a minor burble of protest at my last couple of entries. Isn't "solfege pitch" just another form of relative pitch, I was asked? Although my answer is emphatically no-- not in the way we traditionally define "relative pitch"-- I suspect that by using the term "solfege pitch" I may have obscured my point, which is that the categories of "relative pitch" and "perfect pitch" fail to sufficiently explain the myriad mental strategies with which we hear and interpret pitch and musical sounds. I indicate "solfege pitch" as a separate concept, not because I seriously think that a third category should be established, but because I think that the categories themselves should be abolished in their current definitions. Debating the relative merits of one versus the other is as ridiculous as debating whether it's important to be able to spell words instead of speak them.

It seems that my next step is now to illustrate the various types of aural interpretations that I've been able to identify, and in so doing, create a psychoacoustic model of musical sound. I need to do that in order to design the perfect-pitch component of the ETCv3, and considering my current workload, this kind of summation seems a good way to inch forward with this work as I meet those other responsibilities. In the meantime, between the previous entry and today, I've been rather addicted to Chordsweeper and Interval Loader.

In Chordsweeper, I've made it to Level 6, Round 3-- I think I'm going to have to add more levels, to expand the octave range and instrument timbres, since right now it only goes to Level 7-- and I'm hoping that its theoretical learning goals will transfer well to the perfect-pitch game (the one that isn't written yet). I definitely recognize at least some of these chords absolutely, although there are still relative effects I'm subject to in my attempts.

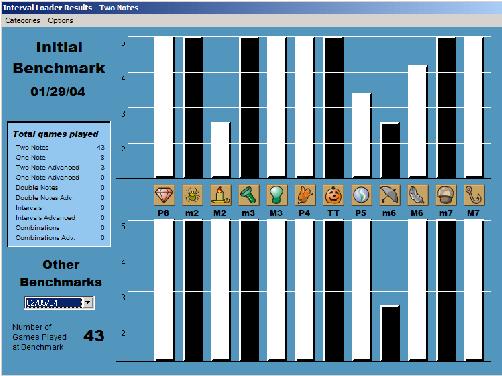
I'm actually surprised at how incredibly effective Interval Loader has been for developing my harmonic relative pitch. Unfortunately, I don't have the hard data from before I began playing the game, which would show how bad I was initially at identifying harmonic intervals-- but I just tested myself today and, as the lower graph shows, the only interval that still gets me is that darn minor sixth, which I keep mistaking for the tritone.

I've never done any kind of interval ear training other than playing this game, so I can safely assume that the game is responsible; I tested my ability a couple days ago by transcribing the melody of a song I enjoyed ("No Girl's Toy" from the Raggedy Ann and Andy musical). Still, I'm also trying to conduct a more formal experiment to verify the results, and I'm also pleased that this initial success, which is fixed-do (C-major), does not immediately transfer to movable-do (here are the results of my initial attempt),

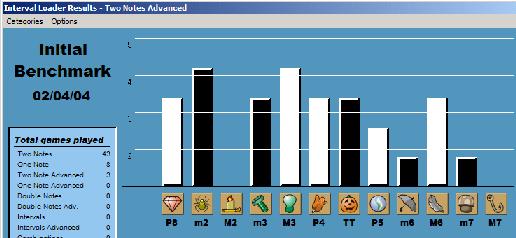
which means that I'll be able to see my progress very clearly. It's terribly exciting to hear a C-major scale degree and instantly know what it is; I look forward to being able to hear any scale degree, in any key, and immediately register its identity. Some initial explorations also seem to indicate that I was correct about the Interval Loader keyboard shortcuts; the skills developed from playing the game with keyboard shortcuts may indeed transfer to playing the piano.

While I contemplate how to begin Phase 9, let me cede the floor to Sean, who recently wrote me about his experience with the Ear Training Companion v2.1. It's most encouraging!

I wrote him back, inquiring more specifically about being able to recognize notes in music; part of the reason for my redevelopment of ETCv3 is that I am not entirely convinced that "pitch recognition" of tones in isolation leads to being able to identify notes as they're flying by in real-time. I also raised the topic of relative pitch, which I feel should be a complement, not an obstacle, to absolute pitch. Here is his unabridged reply:

Sean raises an interesting point-- what is the method by which a person can learn to hear absolute pitches in fast passages? Although I suspect he is correct that it will prove beneficial to practice at increasing speeds, once you get to a sound shorter than 450 ms, the brain is incapable of separating one pitch sensation from another. For that, you need to be able to infer from structural knowledge, and that consideration will drive the design of the third component of v3. This isn't just theory-- I'm still fascinated by the fact that when I play Chordsweeper, the V-chord root always rings out plainly after my mind hears the principal sound of the chord. Ba-dum. My mind simply decides to hear the root tone "later", even though all three notes are played at the same time. That's how I always know it's a V-chord, regardless of its absolute pitch. I asked my roommate if she hears the same ba-dum, and she doesn't; she just hears the entire sound as one.

Transposition:	Features: Same contour, same intervals, different pitches.	BABY SEZ: Same.
Contour preserved	Features: Same contour, different intervals, different pitches	BABY SEZ: Same.
Contour violated	Features: Different contour, same intervals, same pitches	BABY SEZ: Different.

Phase 8a: Learning to Perceive, part 2

November 9 - The shape of rings to come