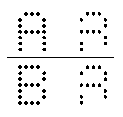
Acoustic Learning,
Inc.
Absolute Pitch research, ear training and more
Just last night, as I was attempting to identify notes, one note came up with an impossibly short decay-- a wood block, perhaps, except it was so short I couldn't even recognize the timbre. Since the note being played was therefore just a quick knock (almost a click) it would have been impossible to tell its pitch using touchy-feely methods. However, precisely because it was so short and unmusical, the vowel sound of "uh" was utterly unmistakable, and I correctly identified it as D.
The fellow with perfect pitch who wrote to me on April 5 mentioned that he heard language sounds in pitches-- but not the same vowels as I've listed. He hears the syllables "do re mi", et cetera, and he was somewhat puzzled by the vowel list which Peter and I generated. I'm not too surprised, though, because of a graphic which I found on Robert Goldstone's site (and have recreated here).
Your mind can complete a partial figure in many different ways. Depending on which perceptual category you're using, the second figure can match either of the complete shapes. You can see it as A or B. By the same token, if you look at the formant chart, you'll see that a pitch frequency can "belong" to more than one vowel. It's entirely probable that you could hear "uh" or "re" from a D-pitch. The reason that I recommend the vowel sounds that Peter and I developed is because we know that at least those vowel sounds are correct. There may be other choices, yes, but at least we know that the ones in the Ear Training Companion are valid and, it seems, universal.
I've asserted that children can be taught pitches as they're now taught colors. If that's so, then the opposite scenario must also be true: if children were not taught colors, they would fail to learn colors. I've wondered about this before; I suggested that perhaps, in a culture whose language only has two or three words for color, adults are actually unable to perceive colors. For evidence, I pointed out how a trained fine artist can see color distinctions that are imperceptible to the average viewer-- but the people to whom I mentioned this idea insisted that it must be a language issue. Of course everyone can perceive any color, I was told, even if other languages don't use the same words as we do to refer to the colors. I found it hard to argue; Pinker does say that "language creates the 'frets' of color", and I've seen evidence that different languages categorize different ranges of color. I didn't have any way to show that people couldn't perceive colors, so I shelved the idea.
Last week, though, I realized that it's not a issue of perceiving colors, but of recognizing and naming colors. After all, anyone can perceive a pitch, even if they can't recognize or name it. And, sure enough, a quick search unearthed the term color anomia.
Patients with color anomia perform normally on tasks that require discrimination of colors but cannot name colors or point to colors named by the examiner. There is a distinction between color perception versus color recognition. A pure deficit in color perception is called Central Achromatosia.
I was surprised but pleased to discover that Diana Deutsch had already drawn this next conclusion, in a paper about absolute pitch:
A lack of absolute pitch therefore appears to be somewhat analogous to the rare syndrome of color anomia, in which the patient can recognize that two objects are of the same color, and can discriminate between different colors, but simply cannot label them.
Not being able to name colors is so rare, that it's called a "syndrome" and given the name "color anomia"-- but being able to name pitches is so rare that it's considered a syndrome, and given the name "absolute pitch". There's no word for people who can recognize and name colors; there's no word for people who can't recognize and name pitches. The terms are easily inferred, though: "color anomia" and "absolute pitch" have their opposite numbers in "absolute color" and "pitch anomia". Isn't it fascinating that color anomia is an affliction but pitch anomia is normal? I hereby declare that the members of the general population are all afflicted with pitch anomia! Let's stamp it out! (Somebody want to organize a walk-a-thon?)
What characterizes the people who have color anomia? Were they never taught colors? Are their brain-scans recognizably different from "normal" when attempting to name colors? Does there appear to be a genetic factor-- do their family members share the condition? Did they spend their childhood locked in a basement? It doesn't surprise me that the condition of color anomia would be extremely rare; "teaching" of color occurs every single day, in formal and informal settings. Some months ago, I was at the post office where I saw a father ask his small daughter to bring him a customs form. "It's the green one," he encouraged her, as she considered the shelf of papers. Children have to make decisions like this every day, in and out of school, because our culture is a culture of color, and with every incident the color names are further imprinted on the child's mind. I'm extremely curious to know what conditions must exist in order to allow a person to grow up without learning their colors.
In my conversation with Dr Weinberger, he spent some time talking about scientific method. "You can throw out the abstract, the hypothesis, and the conclusions of any paper," he said, "and look at the method. That's what scientific experimentation is: if you follow the same methods, you will always get the same result." Well, the Ear Training Companion is a method for learning perfect pitch-- and it's still new, and largely theoretical. It works well for me, but I still haven't been one hundred percent certain that everyone who tried it would achieve the same results.
This is why I was especially pleased when Mike wrote me about his own progress. By practicing once a day, every day, for three months, his results are indeed the same as mine had been. Furthermore, another fellow wrote to me yesterday to describe his experience using the Pitch Acuity drills.
Just to say that I have always considered myself to be tone deaf (can't remember a single tune). Yet from the word go, with your clear and intuitive interface, I have got closer and closer to distinguishing thirds and have even managed to hit on the exact notes on more than one occasion. Truly a remarkable feat for me.
Even though I'm not tone-deaf, when I was doing those drills I had the same delight of gradually being more and more able to recognize notes inside of intervals. It's hard to imagine, now, that I ever had any trouble hearing both notes in a major or minor second! I'm glad I wrote help files as I was going along, so that I could describe the strategies as I learned; now I'd be more inclined to wonder "well, what's so hard about that?"
Today I thought I'd glance at Thinking In Sound, just for a little lunchtime reading, and found myself examining "Perception of Acoustic Sequences: Global Integration Versus Temporal Resolution". (All the quotes in this entry are from that article.) I began skimming it rather lazily, but took greater interest when I spotted validation of an idea I'd mused about before.
The auditory compounds of psychoacoustics and the molecular compounds of chemistry both consist of elements that are combined to form structures with... properties which do not represent the sum of properties of the constituent elements.
So a word isn't just the sum of its parts; a word claims its own singular existence independent of its components. It's true, then, that the nonsense word "gref" isn't just a conceptually different entity from its constituent phonemes. It really is an entirely different perceptual experience.
I was pleased to have scientific validation of my earlier speculation, but I couldn't have guessed what this article would go on to show. As I read further, I was amazed as the article demonstrated-- and the implications of this seem staggering-- that we don't hear the phonemes. According to the article, "...there is a mounting body of evidence indicating that the comprehension of speech and the appreciation of music does not require their resolution into an ordered sequence of components, but rather involves global or holistic organization... phonetic identification and ordering is not accomplished directly but is inferred following a recognition of holistic patterns corresponding to syllables or words." We hear the overall sound, and if we are familiar with its phonemes then we are able to recognize the phonemes within a syllable. Otherwise, we hear only the syllables.
Have you ever wondered where the standard American accent comes from? According to The Story of English, our divergence from the British sound is neither an accident nor a natural evolution. The American accent, it seems, was created by Noah Webster, the dictionary guy. He accomplished this by creating what became, through his efforts, the standard American reading primer, which taught children to read and speak using syllables. It was thanks to Webster that children began to "sound it out"-- in the 1800s, and not before. This syllabic bias is why an American will take the word "Leicester" and want to pronounce it "ly-ses-ter", while a British person will know it's "les-ta". But-- why syllables? Why not the individual phonemes?
In Webster's time, syllables were known as the smallest unit of speech. The word "phoneme" is relatively new-- the Webster dictionary dates the word at "circa 1916", and the dictionary's entry for "syllable" even now contains the definition "the smallest conceivable expression or unit of something". The fact that, prior to 1916, there was no word for "phoneme", by itself seems to indicate that phonemes were not recognized as parts of speech-- but if Webster had developed his method today, he might have stuck with syllables, since there are now "several lines of evidence in the literature indicating that speech is organized initially as syllables, rather than as a succession of phonemes which are subsequently linked to form verbal structures." Here are some of those lines.
Savin & Bever (1970) and Warren (1971) independently reported that listeners could identify a target nonsense syllable in a series of such syllables faster than they could identify a target phoneme within that syllable. ...Subsequent studies involving bisyllabic words have produced results indicating that an initial organization takes place on a syllabic level. ...For example, in French, identification time for the target [phoneme] "pa" was faster in the word "palace" than in the word "palmier", while changing the target to "pal" resulted in a shorter identification time for "palmier" than for "palace".
Another relevant observation is the mislocalization of clicks in sentences... replicated by many laboratories. When a click was placed within a phoneme (taking care to leave most of the phoneme intact), it was found that the location of the click seemed indeterminate, and when required to guess, listeners sometimes mislocalized by a word or two. ...[A] possible explanation is that it is not only clicks that cannot be located within the phonetic sequences forming sentences, but the phonemes themselves cannot be localized directly and are only identified in their proper order after prior organization at the syllabic or lexical level.
Strong evidence that phonemes are not identified directly in connected discourse is provided by phonemic restorations. It has been reported that when phonemes in sentences are completely deleted and replaced by a louder extraneous sound, listeners not only cannot localize the extraneous sound within the sentence... but in addition they cannot distinguish between the illusory "restored" phoneme and the speech sounds that are actually present... Contextually appropriate phonemes are "restored" even when the missing speech sound was deliberately mispronounced before deletion and replacement by a louder noise so that coarticulation information could not be used as an acoustic cue to the missing segment (Warren & Sherman 1974).
It may be safe to assume, however, that all these experiments were conducted on literate individuals. Could it be that, through their life experience, their advanced linguistic skills would have simply trained them to recognize more complex syllable sounds, instead of simple phonemes, as the "units" of speech? No, indeed. Young children demonstrate worse results on phonetic perception.
Several studies have reported that children who are just starting to read find it difficult or impossible to segment words they hear (or speak) into individual speech sounds corresponding to letters in words... Syllabic units... are identified by children at that stage much more readily than phonetic components.
Now, of course, these are children. Perhaps they're just not sophisticated enough in their aural comprehension to be able to break apart sounds into phonemes. The Scientist in the Crib, as well as Thinking In Sound, make the point that speech is not a series of discrete sounds, but a constant flow; it's only gradually that the child learns how to break the sound up into words, much less phonemes. You might think that perhaps we just get better at is as we get older. But this, too, has been considered:
[Morais et al (1979)]... tested two groups of adults living in a poor rural region of Portugal. One group was illiterate, and the other group attended classes in reading as adults. Each group was asked to add the sounds "sh", "p", or "m", to one group of utterances of a speaker, or to delete the sound from another group of utterances. The illiterates could not perform the task, while those with reading skills could perform both tasks quite easily. Thus, it appears that phonetic segmentation, rather than being the basis for linguistic skills, is the consequence of those skills.
Scientists are very precise in their writing, so let me draw your attention to one specific phrase in this quote. They write, "the illiterates could not perform the task." Not "the illiterates had difficulty with the task." Not "the illiterates showed inferior performance to the other group." Not even "the illiterates were very bad at the task." They could not do it. At all.
The human mind, it seems, is designed to hear sounds holistically. This makes sense especially considering the previous article from Thinking In Sound, "Auditory Scene Analysis"-- this article explored the fact that, absent recognizable cues, your mind will generally assume that multiple sounds are from the same source. So, unless you are already primed to hear a chord as a collection of different pitch sources, your mind will automatically assume that an entire chord is a single sound, and perceive it as such. Since the same thing happens with a word, making the order of phonemes incomprehensible, I therefore confidently compare a spoken word-- whose phonemes are spoken in sequence-- to a chord whose notes are played simultaneously.
Our mind's holistic comprehension of sound explains why perfect-pitch ear training starts with Pitch Acuity Drills. I'd heard from one person who had considerable difficulty hearing pitches in the two-note chords, and he wondered: "Do you think it is the level to start from for an average person?" At the time of his request, I had to tell him that I wasn't entirely sure. From this evidence, though, and the acknowledgement that a chord (and its pitches) is perceptually analogous to a syllable (and its phonemes), my answer becomes an emphatic yes.
In order to hear a chord as component parts, instead of a single sound, you need to be able to isolate its pitches. With a two-note chord, there are only two pitches-- the top and the bottom-- and that gives even an unsophisticated listener (like our tone-deaf friend from the previous entry) the opportunity to easily break apart the complex sound. If you took a word with only two letter sounds, like "it"-- which certainly does seem to be a single sound when you speak it-- you could potentially figure out its constituent phonemes just by slowly speaking the beginning ("bottom") and end ("top"). The singing drills accomplish the same thing, allowing your mind to comprehend that there are, in fact, individual components of this single sound. Now, admittedly, although I suspect that this is the level to start with for an average person, it seems probable that having difficulty with two-note chords is not average, and I need to think about how to make it possible for someone to start at an even more basic level.
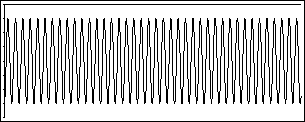
By the way, if you're feeling skeptical about the whole business of not being able to hear pitches except by inference, let me show you something. A single A440 pitch looks like this:
Here's that same pitch, plus... something else.
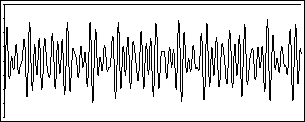
Can you examine this wave and identify where the A440 is, or what's been added to it? Neither can your brain. (Well, all right, it can, but only with practice. Without practiced knowledge, it can't. Just so you know, I added two notes, 3 and 5 half-steps above A440, respectively.)
The holistic-perception effect also explains a number of important ideas I'd mentioned previously. This is why people can identify an unfamiliar vowel or a pitch quite clearly in isolation, as Pinker's "chirpy sound", but then find it impossible to recognize that same sound when it's presented in a word or a chord. Since we perceive the word or chord as a single sound and infer its components, unless we are completely familiar with its components we won't recognize those components. I'm also delighted to realize that this confirms what I was thinking about right at the beginning, which is that a relative pitch listener hears and interprets the pattern of the notes while an absolute listener hears and interprets the notes themselves-- and it resolves the apparent contradiction that the absolute listener hears the entire unique pattern wholly but as composed of the notes, just like IronMan Mike described. This is also why it's easier to hear and recognize pitches when they're in standard chord configurations than when they're presented randomly; since we know the pattern better, we can infer the notes more clearly.
I also think of another thing that IronMan Mike said, and I realize that this may illustrate an important reason for a musician to want perfect pitch. Mike said that he may not be the best musician around, but everybody knows that he's the one whose playing always adds good sounds to the rest of the session. Compare this to the Portuguese illiterates. In any ordinary respect, their language skills were perfectly acceptable. They could converse with you, construct proper grammar, invent sentences to express their ideas and emotions, and in just about every way present themselves as linguistically competent human beings. But when they were asked to make specific, non-syllabic, phonemic changes to their speech-- to add or remove "notes" from the "melody" that they had heard-- they couldn't do it. They weren't just bad at it; they were completely incapable. Their ability to transform language was limited to the relationships between phonemes. By contrast, those who had "absolute phoneme" recognition were able to transform and reinvent the language, in any random way, with total facility. To a certain extent, this must be true of musical performance and composition.
Yesterday's entry prompted some interesting responses!
Pierre wrote to suggest a solution to the problem of a person who can't quite hear even the two-note chords. I was thinking of a simple system of playing notes separately before playing them as a chord, and his initial idea sounded like what I'd already been thinking-- "you read my mind!" I told him. But then he took it one step beyond that simplicity: "maybe [separate notes would be] a good helper to all of us for really complex chords. Sort of blending melodies gradually into a chord!"
I think he's on to something there. His idea reminds me of those old Sesame Street animations, where there'd be a little alien playing a musical sound; another alien would walk in and begin playing a different musical sound, followed by a third alien, and so on, until finally there were a dozen little aliens playing music together. The sound would be a complex mishmash of all the sounds, but since the child heard it put together piece by piece he could (presumably) still recognize all the different sounds within the music. Then, to finish the point, the aliens would walk away one by one and the child would hear the effect on the complete sound. With or without the cute little aliens, this idea could undoubtedly be incorporated into the Ear Training Companion. Although I have not yet learned anything about the Hooked on Phonics curriculum, I'll bet that this kind of process is what they do-- I notice that their home page asks not "does your child have trouble with phonemes?" but "Does your child have trouble with words like 'skate'?" They teach the components so that the combined sound can be more easily understood. (This is in large part why I think it's important to keep coming back to the three-note Pitch Acuity Drills, even while you're identifying pitches.)
Daniel expressed an objection to my conclusion about musical proficiency, referring to Mike's comment that he's "the one that always sounds good":
This I believe comes from no other skill than creativity = originality from the individual. I've played in many bands and am average minus on the guitar compared with the whizzes out there. But they play too many notes and there's nothing we haven't heard before. I play "parts" on the guitar that adds a sensation to the sound. These parts have a PERSONALITY. This is creativity. Something that wasn't there before is born.
As a matter of fact the art of composition seems to follow the same pattern. I was amused that Peter almost seemed surprised that I could compose without PP. The reverse seems to also be true. PP will not give you the ability to compose (music of value). As a matter of fact Paul Hindemith, who claimed PP could be learned... said even all the compositional skills in the art of composition itself would not make the person a composer of value.
This is, of course, true of any field; you can have talent and ability that the world would envy, but without skill and creativity to apply your ability you don't have much. The literate Portuguese were able to change the phonemes of a word, where the illiterate could not-- but so what? There doesn't seem to be any artistic merit to changing the word "pickle" to "pishel". An ability to manipulate language components is only as valuable as its possessor's skill in applying that ability.
But I'm not making a comment about creativity or skill. I'm suggesting that having absolute pitch opens up a brand new way to apply your creativity that simply isn't accessible otherwise. Consider a novel: it can be sophisticated, literate, and compellingly told, yet never vary from standard word spelling or sentence structure. You would never say that the person was not a talented writer, and you wouldn't attempt to argue that they weren't an extremely skilled writer, just because their writing conformed to known standards; in fact, that would generally be considered evidence of the writer's talent. But think about how Walt Kelly, creator of the comic strip Pogo, famously invented sensible nonsense, such as a "mechaniwockle man" or a "porkypine", and used these terms to great comic effect. He wrote perfectly comprehensible language, but its calculated phonemic misrepresentation created a specific artistic impression which couldn't be accomplished through standard syllabic structures.
It's this kind of opportunity which, I think, having absolute pitch makes possible in music. Unfortunately, I'm not familiar enough with classical music to suggest any obvious examples-- but perhaps you have already thought of your own, and Rich has previously speculated on a phenomenon which may be related. Now, admittedly, I don't know if this would be entirely dependent on perfect pitch. Just as phonemic inference and manipulation improves though increased reading ability, perhaps pitch inference and manipulation improves through increased knowledge of music theory-- but it seems at least as likely that perfect pitch would make you more able to hear and create non-standard, but perfectly appropriate, musical performances and compositions. Perhaps perfect pitch lets you bend the rules of music theory that much more effectively, in ways that relative listening wouldn't have suggested.
Still, this is entirely speculation. The important thing is yesterday's main point, which is a heavy one-- that the chord, not the pitch, is the standard unit of musical perception. I'm glad to have that idea in my head as I continue to explore.
Fortunately, Rich has come to my rescue with a musical perspective to supplement my linguistic perspective.
The concept that the English accent evolved from spoken [language] whereas the American accent developed as a result of sounding out words from syllables based on their written spelling... is interesting. I wonder if we can't infer a parallel to the development of equal temperament from the natural harmonic overtone series. Take a natural sound, force it into a useful but rigid system and then start to use that system as the basis of sound generation. Take a major chord, for example. The fifth is almost exactly the second overtone of the root, but the third really isn't all that close to the fifth overtone of the root. However, we are accustomed to the sound, so our ears forgive the variance. Isn't this a bit like accepting "ly-ses-ter" as the pronunciation of Leicester when the original pronunciation was actually "les-ta"? (Not so coincidentally, I'm a Bostonian, and the Boston accent is really a hybrid of the American and English accents, and in particular names of places to this day retain the English pronunciations. We have a Leicester (les-ta), Worcester (wus-ta), and my hometown of Haverhill (hav-ril).
But this, then, becomes an interesting argument for more refined perfect and relative pitch training than what has been taught historically. I personally think that there is amazing musical opportunity in exploring other temperaments and blending eastern and western music. In 1994 Page and Plant did that "UnLedded" thing and performed different arrangements of Led Zeppelin songs. "Four Sticks" and "Kashmir" were standout performances. Why? Because they incorporated an Egyptian ensemble which included the Middle Eastern strings playing the non-western intervals (i.e. the quarter-flat 3rd). It's like the original versions of those songs were pronounced "ly-ses-ter" but the new versions were pronounces "les-ta." Now, not everyone would agree, but I think the latter is a much more pleasing pronunciation, just as the version of those songs with the non-western harmonies sound amazing. But like the illiterate Portuguese people, I could never reproduce that sound because I'm not trained for it. Perfect pitch training is a path to that perception. As you have said before, you didn't confuse C with C#, you confused C with G... it's this type of listening and training that will benefit everyone who uses sound.
Bravo. Well said. As I was considering my reply to him, I looked at his examples of Bostonian pronunciation, and I realized that the English approach to these words is also syllabic-- just divided differently. That is, if you took the individual parts separated like this
Leice - ster
Worce - ster
Have - rhill
and accounted for the fact that the British "r" sound is different, an American would pronounce them the same way. Well, almost-- the first word would probably be "lice-ter" instead of "les-ter", but I'm sure you see what I mean. This underscores the difference between interpreting a written language from units of speech versus interpreting a spoken language from units of writing... and, I think, strengthens Rich's point. What happens if you approach music theory as someone who can already hear certain harmonic patterns? What happens if you approach music listening as someone who already knows, theoretically, what to expect from the sound? The results are different; ideally we could achieve all-of-the-above.
I forgot to include an important fact in my last few entries. I had told you that the phonemes in a syllable are not heard, but inferred. But they are spoken in sequence, and we certainly seem to hear them in proper order... so why am I saying we don't hear them? Intuitively, it doesn't make sense. But it's a sequential illusion, and the answer lies in the latency of the sound. Here's why.
When four unrelated sounds (tone, hiss, buzz, and the speech sound "ee") are presented at matched levels of 80dB, listeners cannot identify the order of the sounds at item durations of 200ms. Even when all four components could be heard clearly and individuals could listen to the recycled sequence as long as they wished, groups of 30 college students could not identify the order at levels above chance... Listeners reported that the order seemed frustratingly elusive, and were generally quite surprised that items could be heard clearly and yet could not be ordered. A subsequent study found that the threshold was between 450 and 670 ms/item... (Thinking in Sound, p 40)
In order to have its own temporal identity, a sound must last for 450 milliseconds. (If that doesn't seem like a long time, remember that you can say "one Mississippi" in only 1000ms.) When you hear the syllable "plink", your mind is unable to create a sequence from such a rapid succession of individual sounds. As far as your mind is concerned, the phonemes arrived simultaneously. This is what I forgot to mention before.
I suspect that this is why it's often difficult to comprehend speech that has been slowed down. If it's slow enough, we can hear the phonemes separately-- but without syllabic patterns, the language loses its meaning. Now that I think about it, this is pretty obvious... speak a word as its phonemes instead of its syllables, and you'll see. For example, say "s-ih-ull-uh-buh-ull". It's practically nonsense. If a listener made the effort, they could stitch it together and reconstruct the word "syllable", but if they hear "syl-la-ble" they instantly understand what you've said. When we hear a word, we're listening to syllables, not phonemes.
When we hear music, we're listening to patterns, not pitches. Diana Deutsch's "Mysterious Melody" deliberately destroys its pattern. By varying the octaves of each pitch, we're forced to hear the song as a succession of individual events. Without a melodic pattern we have no idea what we're listening to.
This example reiterates the difference between "absolute listening" and "relative listening". But this time I want to emphasize that relative listening is simply our normal, human way of hearing-- in language as well as music. As the Portuguese experiment illustrates, being able to "hear" phonemes within syllables is just as exotic a skill as being able to "hear" pitches within melodies and chords. The difference is that every literate person has been trained to name phonemes-- but nobody is trained to identify the sound of pitches.
What is the learning goal of perfect pitch training?
This is what I've been thinking about all week. I've been on vacation, talking with each of my parents, who both have extensive experience in adult education. I've asked them about how to present educational materials to adults, how to create effective language instruction, how to conduct progress measurement, and how to generate practical results. Their answers kept returning to the same question: what is the training goal?
The answer is simple, but staggering: to be able to read, write, and speak music as easily as language. To comprehend music as though it were a language. I feel overwhelmed by what this answer implies for a perfect pitch curriculum, and I've been struggling to stratify and simplify.
I'll have to stretch my thoughts out over different entries, because the more I try to pin this down and condense it into a single topic, the more it slips away and breaks apart. For example, given that the training goal is not to name or produce a note from memory, I'm immediately faced with a barrage of new issues. Why, then, is it important to learn notes? If the true representation of perfect pitch ability is not note-oriented, what does that imply about the supposed classification levels of perfect pitch (with "AP1" as the top level), or any conventional methods for recognizing and assessing perfect pitch ability? Is a note-recognition bias actually harmful to the learning process? Could a more complicated procedure yield more effective results? Yet if it is more complicated, then it must be much more complicated, as one reader recently explained to me:
[With] pitches, you only have 12 to work with... chords on the other hand have many more permutations. the C major chord has at least 3 permutations and each inversion sounds different from each other. You will have to learn 3 variations of the same thing, and for what? to get to a C pitch?
For what, indeed? And that's just one example of how my thoughts have been developing this week. Each new idea seems to give rise to a dozen fascinating new questions. I'll just have to address them one at a time.
I have found the model I expect to use for future perfect-pitch training. The model is that of phonetic reading. I've mentioned Scientific Learning before, because I was intrigued by their online tone-recognition games; but-- now that I have drawn a direct parallel between pitches and phonemes, chords and syllables, arpeggios and words, music theory and grammar, musical composition and linguistic expression-- their methods, and the methods of other phonics-based learning, seem entirely applicable to perfect pitch.
Their on-line book, Why It Works (now removed), is fascinating if you keep the analogy in mind. The book opens (after an obligatory introduction and credits) with this statement:
Decades of research in the fields of education and cognitive psychology have shown that the following skills are critical to learning to read proficiently:
- Phonemic awareness
- Letter-word correspondence skills
- Fluent word recognition
- Vocabulary
- Comprehension skills
- Appreciation of literature
Notice how what we currently consider to be "perfect pitch training" occupies only the first two tiers of this model. Although, psychologically and physically, I still have much to discover about the relationship between perfect pitch and relative pitch, it seems very clear to me that relative pitch and absolute pitch not only do not necessarily compete with each other, but that learning complete absolute pitch may not be possible without relative pitch training. Those people who are assessed as having "AP1" are generally described as having the ability to recognize and identify a pitch regardless of its context; but that context includes-- no, requires-- a vocabulary of musical comprehension. They need to be able to hear a chord and "extract" the pitches, literally, from their understanding of which pitches would comprise a chord of that particular sound. I've suggested that musical training may cause perfect pitch because that's the only form of auditory training in our culture. That must still be true for the reason I said it, but I hadn't considered how, once perfect pitch had begun to take root, it could be the relative-pitch training-- the language training of music-- which encourages perfect pitch to develop fully.
You need to be familiar with the larger structures in order to skillfully identify their components. On the Scientific Learning site, they make an example of the words cat and bat. "If a child cannot identify [phonemes] in spoken words, if he cannot hear the 'at' in 'cat' or 'bat', and hear that the difference lies in the first sound, he will have difficulty with decoding and thus reading." "Cat" has three phonemes-- and a triad has three notes. An unsophisticated listener will hear only one sound in either grouping. The Sci-Learn site further explains how, in words which have multiple phonemes, the child always finds it easiest to pluck out the very first phoneme that they hear; this experience seems identical to hearing only the "top note" of a chord. In any case, if you know the entire word cat, you will be able to quickly name c and at when you hear the single sound; and, if you know a perfect fifth, you will be able to name C and G when you hear them together.
You don't need to study written language to recognize the difference between cat and bat; likewise, you don't need music theory to learn the sound difference between a perfect fifth and a perfect fourth. But you need to learn this difference, because the sensory experience of hearing the word "cat" is totally different from hearing the separate sounds "kkkk, aaaa, tttt". Even though the sounds seem to come in sequence-- and, in the case of extended sentences and words, they do have a discrete order-- it's still an entirely different experience. While I was on vacation last week, I was writing back and forth with an Australian fellow who'd asked me why it took so darn long to learn perfect pitch; as part of our conversation he offered a very interesting observation.
I made a discovery yesterday, or should I say I realized something important. I was thinking about your "cat" analogy and at the same time, was thinking that by now, I should just hear a song and should be able to id pitches. I attributed that inability due to shifts in my tonal center. But your "cat" analogy somehow struck me as something very important. Then I realized that when I hear a chord, even though I could break it down, I still have to think about the pitches instead of them jumping at me. Using your cat analogy, I started playing arpeggios and sure enough, they were no better than chords! Using the functional ear trainer, naming notes was child's play but hearing arpeggios, I couldn't id the notes. we-ll I could but I had to think about them... hard if I might add. I now have to include this exercise in my training. In light of this, may I suggest that you include in your ETC some exercises in arpeggios.
His comment was timely; that day, I had been talking with my mother about how she taught me to read. I was only two years old. I've known for a long time that she spent many hours tracing my chubby baby finger on each letter of the alphabet, while speaking the sound of each-- but I only recently realized that I didn't know how she managed to translate the alphabet into reading skill. Even if phonetic-reading programs had been around back then (which they weren't), the phonetics companies readily admit that the phonetic approach is for children who want to read better than they already do, not for children who can't read at all. When I asked my mother what she'd done, she said that she'd taken a "holistic" approach; she would take me in her lap and read to me, slowly, and occasionally she would stop and encourage me to pick up where she'd left off. Whether or not she urged me to "sound it out", her strategy was clearly not phonemically-oriented-- and it was certainly very effective.
So I had been trying to picture how that would translate into perfect-pitch training, and an arpeggio exercise of some type seems to be the answer. What type, I don't entirely know yet, but I am intrigued by a strategy that Frontline Phonics uses. Once they have drilled the child in certain specific phonemes and blends, they present the child with a story to read-- and that story is written, from beginning to end, with only the sounds the child has just learned. Perhaps I can create a similar reading exercise for perfect pitch. That would have to be an arpeggio. Although the Ear Training Companion currently contains exercises which allow you to ID pitches in three-note chords and three-note arpeggios, and has a twenty-note "speed drill", there should also be some way that musical phrasing can reinforce, "holistically", the pitch sounds that are being studied, the same way that reading "holistically" reinforced the phoneme sounds in my mind.
Perhaps perfect-pitch learning should also include the visual coding of standard musical notation. All three of the models I now have (Scientific Learning, Hooked on Phonics, and Frontline Phonics) agree that phonetic comprehension and reading are inextricably intertwined. Although, in the ETC software interface, the piano-keyboard metaphor was properly replaced by a pitch circle, that doesn't mean musical notation wouldn't be useful for an exercise like this one.
This isn't the only new exercise I'm thinking about. Let me backtrack to naming notes, and the first level of reading progression, "phonemic awareness". This is separate from "letter-word correspondence skills." Although these two levels seem like the Pitch Acuity and Note ID drills, these levels are of reading skill. When they say "letter-word correspondence", they don't mean matching the sound of a phoneme to its name; they mean matching the sound to the written word. In language, the sound of a phoneme is its name, but in music, the sound of a note is not its name-- and this means there is an intermediary step between pitch acuity drills and note identification.
That is, there must be a level which involves identifying notes without using their letter names. This doesn't have to be just "same" or "different" drills, but games which involve recognizing and remembering specific pitch sounds in order to score points. The folks at Brain Connection have the right idea, I think, with the games they've created for their "teasers" page-- especially in the "Sound Discrimination" section-- although of course they never considered perfect pitch. It's possible that this type of exercise could accomplish the most problematic part of the perfect pitch training, and that is simply making the student understand what they're supposed to be listening for. When you're actively, desperately, trying to hear some special thing that some people refer to by the confusing term "pitch color"-- and this thing doesn't literally exist-- it's not easy to understand that all you need to hear is that the pitches sound different from each other. But if you were playing a game, surely you'd have to notice the difference between the notes just to be able to complete the level.
I don't know if you've noticed the nasty little conclusion lurking in all of this excitement, but I've been grappling with it all day today and yesterday: the possibility that perfect-pitch training, all by itself, may not teach you perfect pitch. If, in order to have "AP1", you need to have relative-pitch training and music theory and note-reading skills and arpeggio training, and so on, then no available single method can possibly get you there. I realized, quite suddenly, that Nering's experiment (and possibly Rush's) had two flaws, one of them potentially fatal. Flaw number one: she only asked students to name notes in isolation. It would have been interesting to know if the students showed improvement identifying notes in melodies or chords. Flaw number two: although she had experimental and control groups who did and did not do the "perfect pitch" exercises, all of her subjects were music students, and all of them had musical training in addition to the perfect-pitch training. This flaw is fatal, because it introduces the possibility that the system she is testing doesn't have the ability to take anyone beyond the ability to name or recall notes in isolation. It's possible that the success stories you've seen advertised, of people who claim to have achieved "full" perfect pitch, reflect the results of people who are already sophisticated musical listeners, and whose ordinary musical training-- not the exercises-- is actually what gave them their success.
Nonetheless, even for less sophisticated musicians (like me!), there's still value in being able to name and recall notes in isolation. I was thinking about this especially as I was coming home from work today; I noticed how easily I was able to recognize and name all the colors around me. I've never received any serious artistic training; I don't know a secondary from a tertiary on the color wheel. I don't know complimentary colors, and I don't know which colors you mix to get other colors-- but I can name any color you point to. And that does come in handy. I can think of practical musical reasons why I would want to be able to do the same with pitches-- and I'll bet you can too.
It's been bothering me-- why are notes in an arpeggio difficult to identify? In an arpeggio, the notes don't all arrive simultaneously, like a single chord. The notes are temporally distinct, and physically separate, yet often as difficult to identify as those in chords. For some reason, the mind groups an arpeggio into a single unit, and must be coaxed into assigning individual identities to the pitches. From Thinking In Sound, I believe I've found a clue to that reason, as well as an answer about why "pitches move".
It's ironic that I've been wondering why pitches move, all this time. I've known that the sense of hearing exists to detect movement. Why should it seem so strange that pitches move? In Thinking In Sound's chapter on attention and temporal organization, they made the case quite plainly, and I was stupefied that I hadn't seen this amazingly obvious fact before.
[F]requency or intensity changes are gauged relative to their time spans leading to a continuous motion-like experience. Frequency motion trajectories... can direct attending along paths of implied motion... tend[ing] to follow coherent space-time paths such as those traced by the trajectory of a tossed ball rather than incoherent, i.e. irregular, paths. Similarly, smooth ups and downs of fundamental frequency in speech or music reflect these motion-like properties. (p80)
With the concept of implied motion, there's suddenly a context for the metaphors of relative pitch. Higher and lower, "distance" between notes, and pitches "moving", can be attributed to the presence of an implied object. Any sound-emitting object will seem to change its frequency when it moves-- like the familiar Doppler effect, in which the sound of an object rises or falls as it travels relative to your position. All you have to do is imagine that a note sound represents some abstract object, and when its frequency changes it has "moved" from point A to point B. Think of the cartoon sound of a bomb falling; the slide whistle moves from a "high" position to a "low" position. Although there is no physical object to which a musical note can be attributed, there is an implied object, and an implicit motion which can be measured.
In real life, you can easily guess the position of an object by localizing its sound. Right now, if I close my eyes, I can tell you that my computer is about three feet to my left, and as I hear a car drive through the alleyway I can point to exactly where it is and tell you how far and fast it's traveling. This is just ordinary human hearing, and it is the most normal way to hear notes. Multiple notes, played separately, are like that car driving through the alley. They appear to be a single implicit object that's moving from one place to another. If you have familiarized yourself with the "ruler" of the musical scale, you can judge the "distance" that a note has traveled.
When we hear a simple arpeggio, our minds group the notes into a single event. Even though the notes arrive separately, we still are more inclined to consider the pattern of their "movement" rather than the individual points of the journey. Perhaps this is why notes in a series may "pull" on each other-- and why, if you're not sensitive to how things should move, you don't feel that "pull"-- for the same reason that we'd be surprised if a ball, once thrown, stopped in mid-air or veered at a crazy angle. We know how a ball is supposed to move, so we're surprised if it does anything else. But we do see one ball moving through time and space. It seems to be because of our ability to perceive patterns and movement that the notes in an arpeggio are, indeed, stuck together.
Now, finally, I'm revisiting Harmonic Experience, and at the beginning of the book Mathieu reintroduces an important perspective about harmonic interaction versus melodic distance. Two notes are "an octave apart" when the frequency of one is double the other, in a two-to-one ratio. But the word "octave" comes from eight steps in between the notes, not two.
[O]ur word octave is culture-bound, appropriate to the music we Westerners are familiar with. "Twice-as-fast" or "2:1" is the proportionate-- or harmonic-- name for the "starting over" effect, which is common to all people. So is an octave a "two" or an "eight"? It is clear that the harmonic name, 2:1 (based on frequency ratio), and the interval name, octave (based on scale steps), refer to different aspects of the same thing.
When I first read this passage, I was merely fascinated by the distinction between the "two" of the frequency ratio and the "eight" of the scale steps. I knew they must be qualitatively different listening experiences, because in some cultures the "eight" is instead a "five" or a "twenty-two", even though the "two" is constant among all humans. It seemed probable that Mathieu was indicating the difference between absolute and relative listening, but I could neither describe nor experience what the difference actually was. This time, armed with sine waves and the concept of "implied motion", I can.
At the author's instruction, I created a drone wave of 220Hz. I strongly encourage you to download this file and use it. When I first began reading Mathieu's book, I didn't do his exercises, and I find now that he was right-- you can't really understand what he's talking about unless you do his exercises. I mean, you can understand the ideas, but you won't know them. You have to experience it, as I did for myself, by singing along with the drone. The author says to "let the expansiveness of the drone's sound, even if it is soft, fill you up. Take an ample breath and... sing the drone's pitch within the sound of the drone." If you actively listen to and sing into this drone, creating a "balance" with the sound, you should feel like you have, literally, joined with the tone and become a part of it. You may have felt this effect before in a tiled bathroom, when you found that singing a certain pitch would resonate and make you feel like you were filling the air around you. Do this for a while with the drone; I think you'll want to, since it's a very pleasant sensation.
Then sing along with the same tone-- at a different octave. You'll demonstrate for yourself the feeling of harmonic listening instead of relative listening. If you sing into the drone at the new octave, you won't perceive the "distance" between the pitches. The drone will merge with the sound you're singing, and you will feel the harmonic blending of the two pitches. You will not feel any implied motion between the two pitches; you may not even hear two different notes. You will simply feel the single sensation of the harmonic experience. Once you become familiar with this blending, you don't even have to sing at the same octave to sense it. I just now tried singing different pitches over the drone-- B, G, C-- and I found that I could feel each blend as a unique single pattern.
Mathieu recommends an "ah" vowel for when you sing, because it "sings well". This is undoubtedly because the "ah" vowel is the most open-mouthed vowel, which creates the least obstruction of the pitch produced by your vocal cords. Remember that all language sounds are overlaid upon, not inherently part of, the fundamental pitch of your voice. The language sound can be generated alone, by whispering-- and, although a pitch can't be sung or spoken without filtering it through some language sound, singing with a wide round "ah" seems to be the closest we can get to fully realizing the raw pitch. [Ever since I learned that language sounds are fixed-frequency, my perception of vocal music has gradually altered; now, I can listen to a singer and seem to perceive their words as a separate line, spoken in addition to the pitches they're singing; and the sung pitch has no linguistic value. I wonder if I really am hearing the formant set and the fundamental pitch as separate events.]
It's my impression that this is the difference between absolute and relative listening, in practice. The absolute listener senses the harmonic interaction among pitches; the relative listener judges their implied motion. The question which remains: are these different interpretations of the same experience, or are absolute and relative listeners each ignoring a different type of information? There seems little question that the instantaneous recognition which allows a person to identify an interval is a harmonic perception-- are harmonic and relative listening "different aspects of the same thing", then, as Mathieu suggests, or are they two different things which seem to be similar? My suspicion is that the harmonic event is initially the same thing, for each listener, as a combined sensation; but its pitch meaning is interpreted differently-- one interpretation as harmonic sounds and the other as implied motion.
I suppose I should have expected this. Whereas books like Thinking in Sound attempt to identify and define specific aspects of the hearing process, Harmonic Experience is broadly philosophical. Its bases of discussion are not the concrete results of experimental proof, but demonstrative exercises which generate subjective (if consistent) responses. Consequently, I'm not having the same "Eureka" moments that the other, denser books provide-- which translates into fewer, shorter web updates. But it is fascinating reading, nonetheless, and provides critical insight; in the first part of the book, he's unwittingly provided a literal explanation of what some have called "pitch color" (and which I just call "pitch"), and possibly provided a bridge between absolute and relative pitch.
Mathieu has quantified the feeling of musical sensation as frequency ratio. Sing along with the 220Hz drone wave in unison, at an octave, at a twelfth, and at a fifth, and you'll feel the difference between 1:1, 2:1, 3:1, and 3:2. This isn't exactly the same experience as pitch, but it's close, since this harmonic sensation is a single event-- a unique blending of sound, rather than a "distance" to judge. And, just like a pitch sensation, you won't be able to describe exactly why or how these sensations are different from each other; you can only feel it, and struggle to explain what you so clearly feel. There's something undeniably different, and unquestionably recognizable, about each of these frequency ratios.
A few months ago, I corresponded with a reader about frequency ratios. This fellow wanted to convince me that people with absolute pitch don't hear music absolutely, because he defined music as frequency ratios. Everyone must be listening to relative distances, he insisted; if they weren't, then they wouldn't hear a melody. Neither he nor I knew, at the time, that frequency ratios can be perceived in two disparate ways. Mathieu takes pains to emphasize this point.
[A] scalar fifth is harmonically 3:2. Truly realize this, or the eyes are guaranteed soon to glaze. You must be satisfied in your mind that the numbers five and three are being used to measure different dimensions of the same thing. Which dimensions? The answer is "scalar distance and harmonic ratio." (This opens the larger question, "Why is scalar space additive and harmonic space multiplicative?" which is a question I cannot answer.) (p25)
But we have an answer to Mathieu's question. Scalar space is additive because it represents implied motion, which is linear. Harmonic space is multiplicative because it involves the combined interaction of pitch frequencies, which are logarithmic. You could listen to a frequency ratio and have no impression of distance; you could hear the "three" and have no awareness of the "five".
When listening to music, an absolute listener could hear a "three" where the relative listener hears a "five". Even when the notes do not arrive at the same time, they're interpreted as a single perceptual unit, and can be resolved to "three". But it's true that even if we hear different aspects of the frequency ratio, we all do hear the same frequency ratio.
In the case of the perfect fifth, that ratio is 3:2. The "fifth" pitch frequency has three wave cycles to the other note's two. Mathieu illustrates the 3:2 cycle ratio literally, with a rhythmic beat, so you can feel how the ratio works. He tells you to tap the beats of the 3:2 as a "cross-rhythm". This graphic shows how you can do it, by "thinking" the six-count in the upper line while tapping the middle and lower line with either hand. This beat pattern is the 3:2, although (as a sound wave) it occurs much faster than we can tap our fingers.

I find it hard to tap 3:2 as a cross-rhythm. Each of my hands keeps trying to jump in on the other's beat. Perhaps if I were a drummer it'd be easier. But if I allow myself to tap both lines as part of the 6/8 rhythm, abandoning the "one-two" of the bottom line and "one-two-three" of the middle, it's incredibly easy, since I can collapse the two beats into a single irregular pattern. Even without the 6/8, I can make it easy for myself by thinking of one beat as a response to the other (such as bum, bum-ba-bum on the three-count). I suspect that my inability to separate the two beats into two simultaneous-but-separate patterns is parallel to a relative listener's inability to identify pitch sounds when they are not in isolation. There is no "absolute" frame of reference to grasp the separate beats as themselves, so a relative context transforms two conflicting patterns into a single comprehensible unit.
This example seems to explain the phenomenon of "absolute relative pitch", which is what the Bruce Arnold one-note method teaches. I've often wondered why our minds get "tuned" to a key signature, which makes all the notes sound different, even when they're the same notes in different key signatures. The fact that I can't keep two dissimilar beats simultaneously running makes me suspect that the mind can only easily hold on to a single pitch-beat framework, and this illustration shows that each pitch's beat-pattern is relative to the frame of reference. If you favor the middle rhythm, you're synchronized to 3/4, and the two-tap is off-kilter. But if you're grounded in the lower rhythm, you're tapping 6/8, and the middle beat is out of line. By the same principle, if your mind is "tuned" to F-major, an E-natural will mesh differently with that beat pattern-- the pitch pattern-- than it would with C-minor.
Is there a connection between rhythmic beat and pitch interval? If you sped up this rhythm to a cycle of 200Hz or so, would you hear a musical interval instead of a percussive sound? Mathieu addresses that question but, inadvertently, says something entirely different about absolute pitch.
Some composers have tried to make the connection by electronically doubling the speed of the cross-rhythm until it turns into audible pitches, and then precisely matching up the rhythm with the harmony it generated. But I suspect there is a perceptual canyon between rhythm and pitch we do not cross. The sense of pitch itself may be a breakdown in the ear's ability to process pulses as they become too rapid to perceive individually, much the same way that still images following one another more and more rapidly confound the eye and become, at a critical speed, a movie. (p 23)
In other words, a pitch is "moving" even when it's not being related to any other notes. It doesn't represent a distance, but it has a recognizable velocity. I had previously wondered why single movements produce single pitch sounds, and I hadn't considered that a pitch is representative of the instantaneous velocity of that movement. If you clap your hands right now, you'll find that clapping them swiftly produces a higher pitch than clapping them slowly, even at the same volume.
Normal listening makes us hear implied motion. I wonder if there's some way to redirect that existing knowledge into hearing implied velocity. Perhaps I'll discover it's like what Alla Cohen teaches. One of Alla's students told me that she describes a single dimension of variable sensation along the pitch spectrum; that dimension seems to be velocity. Since the pitch becomes higher, or "brighter", with increasing velocity, this translates directly to "brightness" in the visual spectrum. Although "brightness" doesn't entirely describe any color, it can help to localize the sensation; perhaps I'll be able to find a way to demonstrate this property in sound with new exercises. The trick will be to cause you to listen harmonically for "brighter" and "darker" instead of listening relatively for "higher" and "lower".
My brother is an expert in wave physics. As an astrophysicist, his career is studying stars, which he does by analyzing the energy waves they produce. So, over the Memorial Day weekend, I took the opportunity to interrogate my brother about sound waves. After he educated me about general aspects of the physical nature of waves, I summarized my last few web entries for him. I wanted to know if implicit motion and instantaneous velocity could be legitimate scientific descriptions of sound waves. He agreed that yes, my interpretations sounded literally accurate, with one necessary clarification.
He frowned at my use of the term "velocity" to describe a pitch. A waveform is defined by its three properties: frequency, amplitude, and velocity. To a physicist, velocity is the speed at which the wave travels through a medium-- but my term "velocity" defines the sound frequency. If I want to use the word "velocity", he told me, I must emphasize that I'm not referring to the speed of the sound wave. The "instantaneous velocity" I'm talking about refers to the speed of the movement event which defines the pitch frequency of a wave. As if that weren't confusing enough, he warned me, there is a third meaning of the word "velocity".
The word "velocity" also describes the rate of change of a frequency. My brother complained that the term was imprecisely applied-- "It's more of an acceleration than a velocity." But I was elated when he mentioned it, because it was immediately clear that acceleration is a critical feature of pitch movement.
Acceleration helps explain why the same pitch sounds differently depending on what preceded it. When a pitch moves, it travels along scalar steps, which is a linear (additive) shift. But its motion also an acceleration or deceleration of frequency, which is a logarithmic (multiplicative) change. The implicit object doesn't simply move back and forth, in a simple reversal of motion; when "rising" in pitch, the object gains energy, and when "falling", it loses energy. If a pitch moves up from C to E, it shines with the energy it's been given. If a pitch moves from G to E, it's dulled by the energy it's lost.
This energy effect could be what makes it more difficult to identify notes played in a melody. When I play notes separately, I have no trouble identifying them, but when I play them in sequence it's tough. I can see now that the confusion doesn't have to be because of the note's specific relationship to the previous one; rather, the mere fact that I traveled to the note makes it a different sensation from having started at the note.
Acceleration is also probably why a relative listener feels an emotional "lift" or "drop" from an ascending or descending scale. While ascending, the "object" speeds up, and descending, it slows down. Think of driving in a car, or riding in a roller coaster. Which is more exciting: accelerating from 10 to 70mph, or decelerating from 70 to 10? Take a moment now to imagine how you'd feel at each speed, and how you'd feel as you changed speeds, and how you'd feel when you hit the new constant speed. Pitch motion affects us the same way.
Yet the absolute listener does not sense the "lift" or the "drop"! They only hear the same notes played in a different order. The absolute listener hears no acceleration or deceleration as a note moves from one place to another, because to them, notes do not move. They may sense that notes are brighter or darker than each other (because the frequencies are faster or slower), but they do not necessarily sense the acquisition or dissolution of energy from the implied motion of a pitch. They just hear the same notes in reverse order.
But, interestingly, brain scans have shown that any two sounds, played once and then again in reverse order, do not create mirrored patterns of brain activity. Each pair of sounds is processed as a completely different experience. To illustrate this fact, I had previously used the example of we and you-- "oo-ee" and "ee-oo"-- because it's difficult to hear these words as mirror images of each other (in fact, some people refuse to admit that they are the same!). The absolute listeners may hear the same notes played in a different order, but hearing "the same notes" is an active interpretation, not a default modality.
How do we eliminate the acceleration effect? Although vowel-sound listening helps us to think of musical pitches as separate events (instead of a single moving object), the we-you problem shows that even vowel listening is not a complete solution. In the short term, in my exercises, I'm going to try to apprehend two or three notes as a single unit, because merely thinking of them as "first" and "second" implies moving from one to the next. In the longer term, I suspect that the only way I'll be able to get a decent answer to this question is by learning how absolute listeners perceive note acceleration-- and, since I'd probably have to make them able to hear pitch acceleration in order to ask them questions about it, that may not be an easy answer to get.
Mathieu has told us to think of the numbers three and five, which both describe the perfect fifth, as different aspects of the same thing. Those "different aspects" are harmonic ratio (3:2), and implied motion (5 scalar steps). That's how they're different, but here's how they're the same: if you combine two intervals harmonically, you create an equivalent scalar distance.
Add scale steps or multiply ratios however you like; you'll arrive at the same destination either way. You can use a major seventh as an example. Add a perfect fifth (four steps up) to a major third (two steps up), and you end up at a major seventh (4 + 2 = 6). That's obvious to anyone who knows how to add four and two. The less obvious fact: multiply the absolute harmonic ratios of the fifth (3:2) and the third (5:4) and you still end up with a major seventh (3:2 * 5:4 = 15:8). It seems, in the world of musical pitch, scale steps and harmonic ratios aren't different aspects of the same thing-- they are the same thing.
This isn't theoretical-- you can hear it for yourself. If you play C, G, B, C (tonic, perfect fifth, major third), you can easily hear that you've moved up and down seven scale steps. But if you play C-B, a major seventh interval, you can hear the harmonic fifth-ness and the third-ness lurking inside of that seventh. Mathieu has an exercise that can help you feel the fifth and third "components" of the major seventh. Since this is meant to be accomplished in just intonation, which probably won't match your instrument, I've created the drones you'll need for the C-pitch, G-pitch, and C-G interval, as well as a B-pitch just for reference.

If you do this exercise, you should be convinced that harmonic ratios multiply to create linear relationships. You should also understand how it's possible to perceive a combination of ratios either as a scalar distance, or as a fused harmonic interaction, and not necessarily as both. You should recognize why it doesn't matter whether you play notes as a chord or as an arpeggio, because even when the notes of the major seventh are played as a chord, you can still hear the "4 + 2" that represents the movement of scalar distance.
There are two questions which now boggle me. Since any notes' relationship can be defined by frequency ratios, how do we interpret that ratio so differently-- what is the literal conceptual difference between interpreting a frequency ratio as a distance versus a harmonic fusion? How can the relative listener be trained to reinterpret, as absolute components, the frequency ratio they already know as "distance"? The questions seem to remind me of the hypothesis that perfect pitch training is not about naming notes-- the ability to name notes would be a by-product of recognizing the frequency ratio. I'm not sure yet whether these are giant questions with complex answers, or simple questions with easy answers. I'll give it some thought.
When anyone tells me why they want perfect pitch, their sentiments are consistent: they want to improve their performance and appreciation of music. What they want from perfect pitch training is a better sense of pitch, and a clearer perception of music. Fortunately, that improvement begins to happen well before you can name all the notes.
This afternoon, driving home from the office, I was playing the Stampeders' Sweet City Woman. The title track has always been a favorite of mine; I've listened to it dozens of times. I let the album play through the first half, and smiled when I heard the familiar banjo which opens the tune. In just a few bars, though, my smile began to fade, because the song sounded strangely... thin. Was there something wrong with the recording? I'd recently experienced a disappointment in the CD remastering of the Peanut Butter Conspiracy's first album; my favorite single from that record ("Twice Is Life") had been remixed in a way which totally buried the guitar line. But this album wasn't from a CD remastering; I converted it from the original LP, and it had sounded all right then. In the car, I boosted the bass to maximum; I cranked up the volume; it still sounded just as thin. What could be wrong?
As I listened carefully, I realized that the last time I listened to the song was before I began using the Ear Training Companion. I hear it more clearly now, and that's why it seems "thin". Before, I'd just heard a solid mass of sound; this time, I could tell with certainty that there were only four or five "voices" playing. Lead vocal, banjo, bass, drum, the occasional guitar insertion, and I even heard a subtle vocal line that I'd never noticed before. I kept sifting through the sound as it reached me-- I couldn't believe that a Top 40 song could be composed almost entirely of only three instruments!-- but I could tell that that's all there was. There was no problem with the recording. Perfect pitch training has already given me a more sophisticated musical perception; I don't need to name notes to appreciate that.
But even though naming notes is not the goal, it's fun if you can do it. When I went to see The Producers last weekend at the Pantages Theater, I sat bolt upright when, to launch her audition number ("If You Got It, Flaunt It"), Ulla plunked a starting note on the piano. "That's a C!" I whispered excitedly, nudging my friend Gina. "That was a C she played! That's definitely a C!" Gina congratulated me, then told me to shut up so she could watch the number.
My last web entry provoked the same kind of reaction-- great idea, but so what? One reader asked me bluntly: "How is this going to help me learn perfect pitch?" It's a valid question. It's fascinating to recognize that harmonic ratios and scale steps are the same thing, but what good does it do? I was wondering about that even as I wrote the entry, and I've been puzzling over it for the past few days. I've got a few answers, but it seems likely that this observation is even more important than I can recognize at this point in my research.
If nothing else, the ratio/step correlation may prove to be the linchpin of a new form of perfect pitch training. Currently, all available training demands that the relative listener immediately understand something totally new, and then repeats that thing over and over until it finally sticks. If there's a type of sensation which is recognized equally well by both relative and absolute listeners, then perhaps there's a way to start with something familiar, and then gradually but unrelentingly push the listener over to the "other side" of perception.
Here's an exercise which might spring from that idea. Because an interval is a single perceptual unit, its sound interferes when you attempt to identify the notes within it. Even if you can "extract" the pitches from the interval, the harmonic sound attaches itself to at least one of the pitches. While I heard Sweet City Woman as a single mass of sound, I never heard the background vocal; but once I was able to distinguish the parts I suddenly noticed there was something "left over". I think it will be useful, and relevant, to identify the harmonic sounds of the perfect fifth or major third (to begin with, adding all the other intervals one by one). It seems probable that, once you become familiar with the sound of an interval, you will be able to hear it and the pitches that comprise it as three separate events. And, consequently, you'd be able to identify the notes more readily.
For those of you who were scratching their heads at my last entry, asking "How do I use this?", I should emphasize-- I'm not sure if Harmonic Experience will always be directly and blatantly applicable to perfect pitch. With the academic books, it's easier, because they demonstrate scientifically valid facts about hearing and listening (at least, as valid as psychology or brain research is capable of, at this moment in history). Reading them, I can conjecture if X, then Y. From Mathieu's book, instead of specific proofs, I'm expecting to gain an overall picture of what we experience in sound. Naturally, I'm filtering all he says through the lens of "How does this apply to perfect pitch?", but I think it's the complete picture that Mathieu paints which will prove invaluable to my research, more than the individual points along the way. That's why I expect to write fewer, shorter entries as I'm reading his book-- I doubt that every entry about the book's content will be immediately "useful", but I'll keep writing, nonetheless, to help present that picture to you.
The exercise that I suggested in the last entry is now implemented as "Harmonic Drills". I spent the weekend writing the new routines, and gave it a test drive today-- and I must say it's even more than I hoped it would be. The most comforting thing about the Harmonic Drills, of course, is that you can relax and allow yourself to hear the single sound of the notes played together. After struggling through the Acuity Drills, trying to pull apart the sounds that your mind so adamantly wants to combine, this is a welcome change. However, precisely because you've done the Pitch Acuity drills, you're aware that what you're hearing is a combination of sounds, and with a little mental tweak you can hear the pitches inside the interval.
This awareness will be critical to gaining a more sophisticated level of perfect pitch. It's been scientifically demonstrated that our minds will hear a combined sound and infer its components. The combined sound is processed first. This implies that we must become familiar with the combined sound! I knew that theoretically, which is why I was so eager to write these exercises into the Ear Training Companion. But as I was testing the program, playing around with the different levels, I heard a few remarkable things which seem to validate the theory.
One of these was the first chord of Free to Be You and Me. The Ear Training Companion played this major third (Eb and G) and it knocked my socks off. I mean, it was funny to hear it, since the notes and the banjo-like instrument were randomly selected-- but what really amazed me is that, even though I'd listened to the song recently, and I've heard it many dozens of times in the past, I never had any idea that the banjo was playing more than one pitch. But I played the Eb-G over and over again in the Ear Training Companion, and it was undeniably the opening of the song. I grabbed the Free to Be CD and played the opening, and sure enough, there was the same major third. As I listened to the CD, repeating the opening again and again, my mind kept trying to insist that the G wasn't actually a separate pitch. It kept wanting to think that the G was merely some feature of the banjo's timbre, as it had always assumed in the past. However, since I recognized the major third, I knew that there must be two pitches in that sound-- and, knowing that, my mind obligingly found the pitches for me.
From my testing, I'm also more convinced that harmonic-interval training may be the conceptual bridge between relative and absolute hearing. I found that, if I listen to the intervals as though they were pitches, they have sounds as unique and distinct as the pitches themselves. If that seems pathetically obvious to you-- which it might, if you've done any relative-pitch training-- I'm delighted. I want this to be unbelievably easy for anyone to understand. What was most encouraging is that I recognized the differences between the intervals using the same perception as with which I recognize the differences between pitches. I suspect that the ordinary, relative listener will easily be able to tell the difference between two intervals; after all, that's how we can tell major from minor. And then, once they understand that the difference isn't just "distance", but sensation, that method of sensing can surely be transferred to pitch identification. Directly. Without confusion or mysticism.
On prime-time network television, there are 10 minutes of commercials every hour. This means, of course, that an hour-long program actually runs 50 minutes, and a half-hour show gets 25 minutes on the air. Syndicated shows, in comparison, get 5 minutes fewer than that; the syndicated slots are 45 or 20 minutes per show.
So you may wonder-- when they rerun a prime-time show in syndication, how do they manage to make it fit? The longer shows often delete five minutes of material. In fact, sometimes they write in unnecessary footage just so it can be cut later (On one episode of Quantum Leap, Scott Bakula opened the show by rescuing a cat from a tree as his "leap"; that scene was dropped from syndicated reruns). The half-hour shows can't always afford that kind of excision, so they have another strategy: they speed up the tape. I didn't know exactly how fast until a few years ago, when I had a complete set of original-run Friends episodes and two VCRs hooked up to the same TV. I recorded one of the evening's reruns, cued both it and the identical (original) episode to the first fade-in, and hit play on both decks. By the time the original episode was barely halfway through the opening scene, the rerun was through that same scene, past the intro credits, and well into the first commercial break!
I haven't owned a television set for nearly three years, but my roommate often watches his in his bedroom. Last night I overheard the Friends opening theme coming from his set, and as I listened, the song made me feel uneasy. It sounded anxious, and on edge, not at all like the easygoing slacker anthem I was so familiar with. I wasn't quite sure why, and I kept listening for clues until I realized that it was Tuesday, not Thursday. It was a rerun, and I was hearing the sped-up syndicated theme song. I wouldn't have noticed that if not for perfect-pitch training-- and, having noticed it, it annoyed me.
Today I was at the local Trader Joe's, buying some kiwi-strawberry beverage, when I recognized the Muzak playing an instrumental version of "Can't Smile Without You". I like the song (I grew up with my dad's Carpenters albums) so I began whistling the melody... incorrectly. Irritated, I stopped a moment, listened, and started whistling again. Within three notes I was out of tune. Well, I acknowledged, I'm still new at whistling; maybe I'm just having trouble forming the pitches. I began singing along instead-- yes, I know the words-- but just as quickly found myself on the wrong notes. Startled and frustrated, I stopped. This had never happened before, and was in fact the opposite of my recent experience.
One benefit of perfect-pitch training is that I've gotten much better at harmonizing with my favorite songs. In the past, I've always enjoyed singing along to music, but every single time I'd try to leave the melody and improvise alongside of it, after a few bars I'd discover that I wasn't making up anything new. I was merely following some line in the song I hadn't consciously noticed until I'd begun singing it. Now that I can hear all the parts in a song, I can easily invent something that I don't already hear, and my increased harmonic sense helps me make it sound good. On the way to the store today, listening to Mungo Jerry and the New Monkees (remember them?), I had been particularly pleased with the extra notes and echoes I'd been able to throw in. So what had happened?
I ignored the instrumental music and listened to what I was singing. I wasn't ranging or sliding, and the notes were relatively correct. Where was my error? I suddenly realized-- I was whistling (and singing) in the same key the Carpenters originally sang the song! The Muzak was in a different key!
The timing is good, then, that I'm now starting to take a hard look at relative pitch. I have now experienced the two major complaints about perfect pitch. That is, when people say they don't want to learn perfect pitch, they'll most frequently say that they don't want to be annoyed by a song that's off-key, and they fear they'll have trouble with transposition. Well, friends and neighbors, I can tell you that the danger does exist, and we got to watch out! These problems can be avoided with good relative training, which I don't yet have. Absolute pitch in music informs your relative perception. It isn't meant to replace relative pitch.