(this is a sine graph of a minor second)
Acoustic Learning,
Inc.
Absolute Pitch research, ear training and more
Marguerite Nering, in her University of Calgary thesis, has done an excellent job providing a thorough description of pitch. She says, astutely, "To understand perfect pitch, one must understand pitch," and she dedicates fully 61 pages of text to that exploration even before beginning to consider absolute pitch and her own experiments. Although Richard Feynman would undoubtedly shake his head at my using Nering's report as a secondary source in describing the concepts of "pitch" to you, the body of information Nering has assembled to describe pitch appears to deliberately avoid a definitive single answer to that question, but attempts instead to impress on the reader that "pitch" is a remarkably versatile and incredibly misunderstood word.
The headings of her paper's sections:
Background - 8 pages (which I wrote about in Phase 3)
Scientific Pitch - 38 pages
Musical Pitch - 23 pages
Perfect Pitch - 67 pages
Methodology - 28 pages
Results - 178 pages
Summary - 17 pages
(The Results section is as large as it is because it incorporates all the graphs, figures, tables, and tallies that comprise her experimental data and analysis thereof.)
She bundles some extra "background" into the beginning of her section on scientific pitch, and introduces an interesting term: psychophysics. She didn't invent the word; she credits a 1982 publication by Rasch and Plomb (a publication which is also cited in this paper) for that. Psychophysics, of which "psychoacoustics" is one logical branch, is "the scientific field concerned with the relationship between the objective physical properties of sensory stimuli in our environment, and the psychological responses evoked by them."
In this context, the most significant aspect of psychoacoustics is that there is distinction between event and interpretation: the physical event of the sound's reception, by the bioelectric mechanisms of the ear and the brain, precedes-- but is not a part of-- the psychological interpretation of that event.
On the face of it, this isn't a new idea to us. I've already mentioned how a sound is psychologically interpreted, and that this is largely why perfect pitch can be learned. But Nering disassembles the idea of "pitch" further, into its various applications and representations, both physical and psychological. On this website I've restricted myself to the three-step notion of "sound created", "sound received", "sound interpreted", because I haven't had the research available (or the academic need) to explore that further. Nering's paper has expanded the process to six steps, each with its own unique representation of pitch. I'll report on those later.
For now, I'll mention that I can now recall a middle C consistently and accurately with very little doubt-- not just now when I've returned from a musical rehearsal, but also first thing when I wake up in the morning and have heard no other reference pitches. (I recently wrote about how I recalled the C, but wasn't certain.) I don't always hit it on the first attempt; I mean, before I imagine anything at all, I attempt to instinctively produce a C. Most of the time I seem to be hitting it correctly; but, if I have it wrong, I'm happy to say that I can feel the wrongness of it and, through trial and error subsequently produce the correct note before testing myself versus the piano.
It may seem odd that I would be constantly coming back to the C when I have already discouraged learning perfect pitch by reinforcing a single tone. This is not a contradiction. I am testing myself on the C throughout the day as a complement to my regular perfect pitch exercises. I know when I have the C, not just because I have remembered the correct overall sensation, but I can mentally compare it to other notes which are not C and be certain that I have it right. If I had no other pitch sensations in my head for comparison, I would be less certain because I would be trying to memorize too much!
As far as I know, the "pure concept" is a term of my own invention-- and it's not a very useful term. I was thinking about it last year mainly to discover if there was any worthwhile reason to be thinking about it. Essentially, I defined the "pure concept" as the thing which could not be precisely described as anything except itself. For example, if I described "a disc of metal, stamped with designs and slogans by a government, that is used as payment for small transactions," you'd probably recognize that I was talking about a "coin". A coin is an amalgamation of various physical and symbolic concepts; so, by using words other than "coin", I can describe a coin in a way that leaves absolutely no doubt of what I'm referring to, and you can clearly imagine some meaningful representation of a "coin".
But I wondered-- how do you describe a color? You can string together any number of adjectives you want, and you can't pinpoint it. I can say that green is "cool, smooth, and calm", but so is James Bond. How could I describe a color in a way which left absolutely no doubt of what I was referring to? After some consideration, I realized that I could characterize "green" as a light wavelength, and objectively describe "green" as a wavelength of 510 nanometers. But... that doesn't mean anything. There's simply no mental association between "510 nanometers" and the sensation of perceiving green light. The only way to make someone understand what you're talking about is by communicating the word green. A color simply is what it is.
(Of course, this makes me wonder if there is an even purer concept, of something which cannot be described by language at all, but can only be comprehended through direct demonstration-- but that's an idle thought for later, if ever. I'd ask you to e-mail me if you have an idea of it, but ironically its very nature would make it impossible for you to describe it!)
This "pure concept" was a curious idea, but I really didn't see much point to it, so rather than rack my brain for various other representations of it I left it alone. Naturally, once I began examining perfect pitch, it was obvious that pitch was also a "pure concept", just like color-- though it still seemed just as useless to call it that. However, as useless as the term "pure concept" proved to be, it did make me realize that the literal description of a sound or light wave as "x nanometers" is meaningless to most people. So I was pleased to see Nering's double definition in her section titled Scientific Pitch:
Pitch is a subjective, psychological quality of sound that determines its place in the musical scale.
Frequency is a physical attribute defined in terms of the period of motion, which is the time measured in seconds for one complete oscillation of the body.
She then proceeds to cite examples of how a perceived pitch can change based on its intensity, as well as "the hearing of the observer, the range in which the frequency appears, and the loudness to a certain extent." Nering offers these examples mainly to alert the reader that she's talking about frequencies in this section and will be addressing pitch later.
She characterizes the typical representations of sound frequency. The lowest frequencies, below 16 Hz, are infrasound, which can be felt but not heard (such as seismic waves). The highest are ultrasound, which are generally above 20,000 Hz, which can "drill stone, measure depth of oceans, detect better than X-rays, all silently." And then there's everything in the middle; I like the image that Nering evokes of how "the audible range is full of music up to fundamental frequencies of about 1200 Hz, approximately D6."
Musical pitch has a finite range of frequencies within the spectrum of audible sound. Even though the human ear can perceive sounds higher than 4186 Hz (the highest note on the piano), Nering cites a 1954 study by W Dixon Ward which demonstrated that tones above this level "deteriorate rapidly" and are generally not heard as musical tones. High frequencies are usually heard as overtones, not fundamental pitches, and Nering seems to be saying that even when a high frequency is heard as a fundamental tone, it does not seem musical to a human listener.
To sum up, the three important points to recognize are these:
1. Frequency and pitch are not the same thing; "frequency" is physics and "pitch" is psychology.
2. There is a specific range of frequencies which humans normally recognize as musical sound.
3. Outside of this range, sound frequencies are usually considered non-musical, if they are heard at all.
The first point is not merely a semantic nicety; it's absolutely necessary for us to recognize the significance of psychological interpretation in the perception of sound. If you've been reading the archives that's undoubtedly not a new idea for you, but it's such an important idea that it bears repeating.
The other two points are obviously corollary; nonetheless, they are individually significant. What they both accomplish, together, is to re-emphasize the idea that what we hear is what we interpret that we've heard-- and, as point three makes clear, we are accustomed to hearing some sounds and listening to them in a completely interpretive way, not even letting ourselves be aware that non-musical sounds have a pitch.
I have found myself noticing this more and more frequently in everyday life. Just two days ago, I stepped into the elevator at work and its bell announced each floor that I went past. I suddenly realized that I could feel its pitch. It wasn't just "the elevator bell"-- it was an elevator bell that exhibited a specific pitch. It was definitely a single pitch, and I could feel the sensation of its pitch clearly and strongly. But... I still had no idea which pitch it actually was. It's moments like this which continue to make me confident that it's just a matter of time until I've adequately reinforced the mental associations I need to recognize the pitches.
What I also find fascinating about "scientific pitch" is that frequency is a superset of pitch. There are sound waves which we can't even hear-- although they must have pitch characteristics, we can't tell directly, and in the case of the seismic force we can only feel them. If nothing else, it's interesting to recognize that there is great validity to the study of "psychoacoustics"-- that physical sound is very different from what we construct in our heads.
A final topic, changing the subject somewhat-- Nering states, without reference, that the human ear is "more sensitive to high pitched sounds than low." Since hearing is our mind's interpretation of movement, I wonder if perhaps we're more sensitive to high-pitched noises because those are going to be the leaves rustling and the twigs snapping underfoot as the predator closes in on us. I wonder.
Most of what Nering has written about complex waves and overtones is not new to us, so I'll pick through and find the points which are new-- or at least, a new take on an existing idea.
I wrote very early on that I attempted to identify a guitar note, and when I failed to name the correct note the guitarist commented that I had named the note's strongest partial. Nering cites a study which shows that the overtones of a sound are audible as themselves "if the listener's attention is drawn to their presence." It's interesting to recognize that even so early in the process, I was familiar enough with the note I wanted to hear that I was able to home in on it when it was buried in a complex sound as an overtone. Although I hadn't been deliberately told to listen for the overtones, my imagination found the familiar part of the sound.
It's interesting for a singer to know-- even though it has nothing to do with perfect pitch, directly-- that "it is the overtones more than the dynamics that give a voice or instrument its carrying power." In one of our sessions, my voice teacher explained the concept of what she refers to as "ring"; by raising the upper lip into a kind of sneer, you can dramatically increase the intensity of your voice. The purpose of changing your mouth's shape is to change the overtones it creates; if it's overtones that give you more carrying power, then it's equally important to learn how to configure your mouth when you sing in a particular style as it is to know how to use breath support and posture. If you're a singer, you probably knew that already, if only through your physical training-- perhaps you'll find it interesting, as I do, that you can analyze it scientifically with overtones. I know that some people already have; I read a book called "Voice Tradition" or something and I found it had lots of raw data but sparse analysis.
I've speculated that perhaps virtual pitch is actually created by the physical combination of the overtones. ("Virtual pitch" is Ernst Terhardt's term for the pitch you think you hear when the overtone series of a pitch is presented minus the actual fundamental pitch.) I showed, in sine-wave diagrams that I created with a spreadsheet, that you can remove many of the overtones and still have a waveform that has a period recognizably identical to the fundamental. However, Nering cites five different studies in which the experimenters did something which I slap my head for not having thought of-- they presented different overtones to each ear. The scientists simply played one overtone in each ear, each in isolation, and voila-- the listener heard the implied fundamental of the virtual pitch. This immediately and completely disallows the speculation that the virtual pitch is somehow physically created in the ear. Instead it's a "central neural process and was not brought about by... the ears", as Nering puts it. After a complex sound is broken down by the spectrum analyzer which is the ear, it doesn't come together again until after it reaches the brain. I realized a couple days ago that I haven't even glanced at the auditory cortex; I've been focusing completely on the physical ear and ignoring the brain. This is a grave oversight on my part, because at this point I don't have an image of how the frequency impulses travel from each ear to "combine" in the brain as virtual pitch.
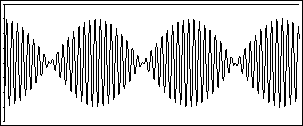
I'm not sure I've even mentioned "beats" anywhere before-- they didn't seem specifically relevant to anything. Acoustic "beats" are what result from waveforms interfering with each other; as Nering puts it, "the resultant sound... [will] become stronger and weaker, giving rise to a pulsating or beating effect." I mean, this is interesting; this is what consonance and dissonance are all about. When waveforms reinforce each other more than they interfere, they beat less, and when they interfere with each other they beat more. That's why dissonant chords have a recognizable wobble-- they look like this:

(this is a sine graph of a minor second)
But aside from being an alternative way to explain consonance and dissonance, I didn't see much use for "beats". The waveform combined, and "beat" against the inner ear, and there we have dissonance. It seemed rather straightforward and unimportant. But yesterday's comment has given some new life to the idea, since I know that pitches presented separately to each ear are combined in the brain.
Tonight I attached some headphones to my computer sound card and used Cool Edit Pro to test this. I put a 220 tone (A3) in my right ear and 247 (B3) in my left. And I'll be darned-- they beat. It's not as pronounced as the combined tone-- the beat of the combined tone is so prominent that it sounds like purring, or rolling your tongue-- but it's definitely there.
And what's more, I was fascinated to read that if the beats are close enough together, the mind averages the pitch. So I created a 220 tone and a 225 tone, each in both channels, and a 1-second segment with a different tone in each channel. Since my perfect pitch ability is still developing, obviously I knew I would not be able to clearly distinguish a 220 from 223 from a 225 just by listening to them separately, so I put them into sequence-- starting with the 220, followed by the combined tone, finishing with the 225, reasoning that if my ear were averaging the two pitches I would hear three notes ascending. And that's just what I heard. Try it yourself.
Of course, I'm delighted to hear this result because it seems to verify what I was saying about the mental overlap between pitches; but even more curious than that is the fact that, when listening to this sequence, I discover that I can choose to hear the sound in the middle either as a single, averaged pitch or as the separate pitches which are its components.
I finally took a look at the auditory cortex. Eep! It's both amazingly simple and terrifically complex. What seems to be simple is the tonotopic map of the brain's primary auditory cortex; what's complex is... everything else. Fortunately, I have only one interest in it right now, and that is virtual pitch perception. I'm fascinated by the fact that when each ear receives a tone separately, the brain will combine them. This seems to suggest that the ear's function is merely to present spectral output to the brain, and nothing is "assembled" until after it reaches the brain. All the things I've been writing about overlap on the basilar membrane and combinations of sine waves is still a legitimate model-- but apparently it doesn't happen in the ear, as I've been imagining it. Frequency synthesis seems to happen entirely in the brain.
It's times like now that I wish I had the resources of some of these scientists. I would love to be able to create my own brain scans! If you've read the secret of lesson one, you know that people with perfect pitch perceive all like pitches as being "next to" each other, instead of separated by eleven other chromatic tones. It appears that the tonotopic map of the primary auditory cortex, however, spans the entire range of frequencies, with each octave indeed separated by all the interlying tones. I would love to see directly if there is some harmonic reaction to each pitch octave within the cortex.
I've offered my own conclusion that, in order to learn pitch sounds, you must compare pitches to each other. I was pleased today to read that hearing isn't the only sense that works by comparison. As we've seen in countless optical illusions, we can be tricked into seeing the same color as lighter or darker depending on the colors it's near; likewise, a pitch can seem higher or lower depending on the pitch which preceded it. Yet, according to first-hand reports, this high/low distortion does not occur in the mind of the person who has perfect pitch. Why not, I wonder? Is this an unusual acuity for pitch resolution, or is it a failure of intellectual synthesis? It seems unlikely to be a failure, if only because the perfect-pitch listener can identify relative intervals by recognizing their harmonic interaction.
The fact that the ear "averages" two pitches that are near enough in frequency appears to verify the idea of pitch overlap-- specifically, why it is that a musical note sounds differently when played in an ascending or descending scale. Although that might seem merely a restatement of what I just said in the previous paragraph, what's important is that it doesn't matter if the physical energy of the previous pitch has completely faded. As the isolated-ear demonstration shows, the brain combines the neural images of the tones it hears even if the tones are received separately. It surely follows, then, that as long as the neural image of a sound remains in short-term memory, it may be intellectually combined with any sound that follows.
According to Nering, the frequency of a sound wave is just one element that determines the subjective pitch perceived by the listener.
A sound frequency, played at different intensities (louder or softer), will result in a different perceived pitch. This is well-documented, and if you've been poking around the net looking for information about pitch you've probably encountered this fact already. Nering obligingly mentions this reason and then moves on to list others. Here's a short summary:
Temperature changes the velocity of sound through the air, so that sounds on warm days are "lost faster" than sounds on cold nights. Humidity causes refraction as sound waves pass into less-dense water vapor, which increases their velocity (and perceived pitch). Formants, which are additional sounds caused by parts of the sound source other than the main source of vibration, can alter the tone and quality of a pitch.
And there are also transients. Nering describes transients as
...the particular way in which the tone of an instrument begins and builds up, for example, the characteristic 'piff' of the flute, or the scratch of the bow in the violin. Possessors of perfect pitch have more difficulty identifying tones on a synthesizer and this is thought to be due to lack of familiar formants and transients.
Her citation for this statement is "Lowery, H. A Guide to Musical Acoustics. New York: Dover, 1966", and I wish I had that publication in my hands right now. Who are the "possessors" that she and he are referring to? Are they people who were born with the ability or people who developed it? The people I've encountered who were "born withs" all insist that they never developed anything, but always heard the pitches-- but the woman I met who said she developed it said with equal emphasis that to her, pitch is where she senses it on her instrument (in her case, her voice), and other musicians have told me how they are plugged in to certain tones on their own instrument.
I would love to know the "level" of the people whom Lowery must have studied. I'd want to know if the people who have difficulty on synthesizer are those who did indeed develop AP as a young child instead of being born with it, and I'd be intrigued to discover if any people who are "born with" would have any trouble with synthesized notes. Because, if what I've been saying about pitch acuity is right, then people who were born with AP would recognize the inherent characteristic of a sound regardless of its timbre, and people who'd developed it in the process of musical training would almost necessarily have attached additional acoustic information (overtones et al) to their mental comprehension of each pitch.
That makes me think that, if you're going to teach perfect pitch to your children, you should take great pains to play notes for them from different instruments, not just their favored instrument, not just their instrument plus the piano, but from all kinds of sources. Let them naturally filter out what does and doesn't belong.
Having described how the sound is created and modified, Nering moves on to illustrate how the sound is physiologically received. I'll recap now, not just for the sake of continuity, but because I'm not sure whether or not I've presented a single complete picture of the process-- I think if you've read everything written here, and followed the appropriate links, you'd pretty much have the process figured out by now, but for clarity and to save you from traipsing all around to find all the pieces, today I'll attempt to put it together for you, at least in summary if not in total.
Here I'm going by my own memory; please forgive me for not linking everything within what I write, but the verification of the things I say can be found, often illustrated with animations and delightfully specific descriptions, on the research page. Nering seems to make a semantic error in her narrative, suggesting that the hair cells themselves "resonate", which they do not. I had been writing back and forth with an engineer who claimed that there was absolutely no resonance inside the ear; although, in order to support his idea, he had to claim that every researcher since 1929 had been duped into following some erroneous model-- a proposition I found difficult to accept-- I was intrigued by his alternate explanations of standing waves and traveling waves, and if the inner ear was structured as he described, I could see how his ideas would have merit.
My research has pointed me in a direction which is different from that engineer's opinion, and I feel adequately confident about my findings to report it to you as the truth-- but my conversation with the guy reminds me that this website wouldn't exist if I didn't firmly believe that a majority of researchers are wrong about the nature of pitch and pitch perception. All the same, I haven't constructed any physical models to test for myself-- in everything I've written so far, I have been relying entirely on the available Web research, the books I've read, and my own psychological experience. I've said before that those who might be of the opinion that I'm "just making all this up" should follow the research links; I add to that that anyone who is skeptical of the available research should do so by looking at that research and drawing an informed conclusion based on what you find, rather than taking anyone's interpretation of that research (including mine) at face value, or decrying research without creating an acceptable and demonstrable alternative. For me, of course, this entire website is intended to present an alternative, and I hope you've felt as excited and educated reading these entries as I've been feeling as I write them. But, of course, if you've any reason to believe that I'm wrong, I welcome your contention; for all the research I've done, there are plenty of sources I've overlooked or not yet examined in adequate detail. If you know something I don't, by all means, lay it on me, baby.
So, having said all that, now I'll present what I have learned about the mechanism of hearing.
The sound is received and channeled by the outer ear. The outer ear is the "pinna" (the part found on the ground in the film Blue Velvet), the auditory canal, and the eardrum. The sound reaches the eardrum, or tympanic membrane (cute, eh?), which moves a small bone called the malleus ("hammer") which strikes the incus ("anvil"), which transfers the vibration to the stapes ("stirrup") that in turn vibrates the oval window to which it's connected. These three bones are what comprises the middle ear, and the oval window is the portal to the inner ear. Now, exactly how these three bones precisely transmit a complex sound, I honestly don't know. Do they move in more than two directions, or do they just strike Morse-code style as a summation of everything that they've received? It appears to be the latter, since everything I've read so far has either omitted the specific description of how the sound wave is transferred through these bones or said, almost dismissively, that the stirrup acts like a piston to represent air compression to the inner ear.
If sound is air compression, you might think it could be described merely as molecules bumping into each other, to the extent that it would seem as though it could be a kind of binary system-- bump for on, don't-bump for off. Of course, this statement is an untenably gross oversimplification-- I've seen a remarkably complex physics paper which presented equations for waves within the ear that might as well have been hieroglyphics for all the sense they make to the average person. However, until I understand equations like that, I will have to accept the simple fact that through this middle-ear structure any complex sound is transferred to the inner ear via the oval window. I find it astonishing-- our bodies are designed to do this sound transference as a basic function of living-- and yet understanding exactly how it's done takes an intensely advanced understanding of mechanical physics.
So let's allow for the moment that a sound wave of a single frequency reaches the inner ear through this system of levers and membranes. The inner ear-- the cochlea, named for its spiralling resemblance to a shell-- is filled with fluid and contains the basilar membrane. Once the stapes vibrates the oval window, the oval window sends that vibration as fluid compression down the length of the cochlea, along the basilar membrane, until the vibration reaches the round window and is dissipated.
In the 19th century, a guy named Helmholtz developed the theory that the inner ear worked by resonance. He speculated that the inner ear was possessed of thousands and thousands of receptors which were like piano strings, such that, when a sound frequency was introduced to the inner ear, it would create response in the sympathetic vibration of a specific receptor cell-- and only in that cell. You can observe this effect in real life by placing a pitch source next to the string of a musical instrument (of the same pitch, of course)-- the string will begin to vibrate in sympathy with the source. In 1929, another fellow-- name of von Bekesy-- discovered that Helmholtz was essentially but not exactly right. Von Bekesy demonstrated that sound is not stopped or "picked up" anywhere within the ear, but that every sound travels the entire length of the ear, and the component frequencies of the traveling wave each affect the basilar membrane in different places.
The best description I've yet seen of the traveling wave is that of snapping a rope. Now, because the rope's stiffness is essentially the same from one end to the other, the wave you create travels to its end without much change (except, of course, for the loss of energy to gravity or friction); but you can probably imagine quite easily that if the rope were frozen at the far end, you could create a massive whip on your end which would result in barely a murmur at the other side. The basilar membrane varies in stiffness from one end to the other, except that the "frozen" part is at the front end, where the sound is introduced to the inner ear, and the limber end is at the center of the cochlea's coil.
Visualizing a rope makes it easy to explain the concept of the traveling wave, but the basilar membrane is not whipped in the same way that you do a rope. You apply a vibration to the rope directly, and watch it wiggle-- but in the inner ear, the vibration travels through the fluid along the "rope" of the basilar membrane; the stapes does not directly vibrate the basilar membrane. Von Bekesy showed that as the sound wave travels through the fluid, the different frequencies of sound affect different places along the membrane's length. Where Helmholtz had been right, he found, was that the places affected were so due to resonance; Helmholtz had been right in thinking that the ear acted as a spectrum analyzer. Helmholtz had been wrong, however, in thinking that any given receptor cell was activated because it resonated with the incoming sound wave.
There are thousands of receptor cells, which aggregately form the organ of Corti, situated on the basilar membrane. Individually they are referred to as "hair cells" because they are clusters of cilia which resemble hairs. As the traveling wave passes along the basilar membrane, the membrane-- and not any receptor cell-- resonates with the wave. This is why the far end of the membrane, which is less rigid than the near end, does not vibrate from the higher energy of the higher frequencies; it's not just a matter of the high frequency pounding more emphatically on the stiffer part of the membrane-- as would be necessary to flex a frozen rope-- but the fact that the stiffer membrane is resonant with a higher frequency, and the more flexible part is not.
Once a specific area of the basilar membrane is resonating, moving back and forth, the hair cells which are on that area are pressed against the tectorial membrane, and in so doing create a bioelectric impulse in each hair cell. The cilia are actually one end of the complete hair cell, and it's been recently determined that the cilia are constructed as a switch-- one position "on", the other position "off", depending on how pressure is being exacted upon the cilia. There seems to be some additional complexity introduced by the position of the cilia in each hair cell, but so far it appears to me that that complexity does not introduce any potential confusion of pitch perception. The hair cell (a term that is used interchangeably with "receptor" cell) is directly wired to the auditory cortex within the brain.
I haven't seen a diagram that attempts to show anything resembling a wiring schematic from cochlea to cortex. However, I have seen diagrams which show frequency mapping along the cochlea, and I have seen diagrams which show frequency mapping along the auditory cortex. I don't know whether there's a one-to-one relationship of hair cell to neuron, but it appears that, in normal physiological structure, the "zap" of the receptor cell travels unimpeded to the associated area of the brain.
And that's where the mystery begins. As you might have inferred from this narrative, once a sound frequency is separated by the ear from its presence within a complex waveform, it travels directly to the brain, and it's only once it reaches the brain-- and not before!-- that tricks of interference and combination occur. I've been discovering this by reading this section of Nering's paper and testing myself with Cool Edit Pro's tone-generation function; it seems to lend much greater support to the supposition that perfect pitch fails to occur mainly because we don't know how to properly pay attention. The absolute-pitch information is right there in the brain, and it only becomes an interpreted event after the brain receives it. Of course, until I receive any further information, I'm inclined to think that the genetics folk have it right in thinking that those who demonstrate spontaneous absolute pitch most likely do have some kind of specific brain structure which impels them to attend to sounds in non-musical ways; but it still seems appropriate to conclude, from all available sources, that this different construction simply makes it easier, rather than possible, to understand perfect pitch.
Nering polishes off her section on physiological pitch by mentioning "subjective tones"-- these types of tones were previously theorized to be caused by physical effect, but have since been shown to be mentally induced.
One of these is the combination tone. I don't think I can describe it better than she has:
Tartini, the Italian violinist, noticed, while bowing two strings on his violin, the production of a third tone which some later referred to as "Tartini's ghosts" but came to be known as a "combination" tone. Many combination tones are produced in a single complex tone, and are the result of the pairing of many overtones.
If you've listened to the separate-ear tone example that I posted here a couple days ago, you'll be nodding your head as you read this quote, imagining how your mind can grab on to the dissonant overtones of a complex sound and average them into a single pitch. According to Nering, Helmholtz decided that these combination tones were not produced by the instrument but produced in the ear as distortions, but another guy named Jan Schouten came along in the late 1930s and showed that the distortion effect was, physically, too minimal to be audibly significant. Of course, if you've listened to the separate-ear sound file I posted here a couple of days ago, you've heard a combination tone for yourself, and you know from your own experience that this averaging effect occurs in the mind, not the ear.
Nering also mentions the summation tone, discovered by Helmholtz, which is exactly what the name implies-- a tone perceived at a frequency that is the sum of the two fundamental frequencies being presented to the ear. Then I perked up when I read
Many believe that the perception of the missing fundamental [pitch] in a single complex tone is a result of the occurrence of combination tones providing a fundamental component to the ear...
because I've speculated on exactly that idea here in these pages. And it continues to be obvious that I just have to keep reading, in order to find out how much of what I've been thinking about is new (if any of it is) and how much has been scientifically considered-- because Nering cites a study conducted in 1954 by a fellow named Licklider. This guy masked the expected fundamental pitch with low-pass noise, and "the sensation of low pitch remained."
But even if the ear is not physically sensitive to combination tones, the fact is that they do happen, and frankly I'm more pleased that it should happen in the mind instead of the ear. In a way, it is kind of a bummer, because this means the occurrences of these combination tones can't be physically tested, and therefore their appearance and effects on the auditory system can't be directly demonstrated or proven-- but this observation treads way back along my lines of thought to support some important earlier inferences. Namely, it seemed reasonable to suspect that people who demonstrated absolute pitch acuity are interpreting the harmonic sounds, and people with "normal" musical perception are interpreting the intervallic sounds (a tip o' the hat to Mathieu for giving me that vocabulary)-- and that learning to attend to one or the other is principally a matter of recognition and practice.
Knowing that the pitch information remains completely raw and uncombined until it reaches the brain appears to offer strong support to this theory. I've learned now from someone with perfect pitch that there are definitely two modes of hearing, that of absolute or relative listening; she says she switches from one to the other when she needs to transcribe, since following music absolutely is "too slow". I also would remind you of the University of California Irvine studies (and others) on absolute pitch in people with Williams syndrome or other deficiencies of intelligence; these people universally have absolute pitch perception. I said earlier on that this was probably because they understood sound more clearly as non-interpretive pitches instead of a more sophisticated musical comprehension. Although it has subsequently been shown that people with Williams syndrome have become unusually competent musicians, it's also true that people with absolute pitch do not necessarily ever need to develop relative pitch in order to be proficient musicians; IronMan Mike is an obvious (and outspoken!) example.
And, of course, the fact that I'm learning it and that it's working tends to "offer support", as well. If anyone wants to do some reading on the plasticity of the brain in acoustic memory, and report it back to me, I'd appreciate it; after I finish this Nering study (and unless I let myself be less verbose, that could be a while), I still have both Deutsch's and Mathieu's book to tackle. I'm certainly looking forward to it!
It seems that in order to successfully identify and recall pitch, you need to be able to do so on any instrument. I've advocated the notion that in order to perceive pitches you need to be able to compare at least two sounds; it seemed to me that, by comparing two pitches on the same instrument, you learn that the pitch sound is separate from the extraneous overtones and frequencies produced by the instrument. When I hear pitches in everyday life, I find that in order to even attempt to identify their pitches, first I have to repeat them with my voice-- and then try to think of how it sounds on a piano. Not good enough, folks.
I don't know if I can adequately describe how pleasant it's been to realize that the sense of hearing exists to detect movement. That thought has made the world so much more interesting! I listen to the water splashing in the shower; I hear a helicopter passing overhead; people stomp on the cement balcony outside my apartment as they walk by. How fascinating it is to recognize that this isn't just "noise"; this is my brain telling me there's something moving out there! I can't see through walls, nor around corners, and I certainly can't see five miles up in utter darkness-- but I can hear through these conditions and more, and I can make shockingly accurate projections about what and where it is. Hearing is cool.
And I continue to wonder what it is we think we're hearing when we hear music.
Ears are all the same. Well, okay, they don't all look the same, but Nering quotes anatomist Frank Howes: "Physical ears are indistinguishably alike and and the great, manifest and indisputable differences in aural capacity must be attributed to powers of the brain and not to physical differences of the ear." And the invariable physical function of the ear is, as you've learned, that of a spectrum analyzer, to break apart frequency sensations and deliver them to the brain. Although we don't know for certain that the ear itself provides no additional information (such as beats or subjective tones) there appears to be a very strong consensus that analysis of those received frequencies happens-- if not entirely, then substantially-- in the mind.
The old question of "If a tree falls in the forest, does it make a noise?" can, of course, be literally answered; the falling tree causes air compression, and that event is the same whether or not there's an aural observer to describe that compression as "noise". But here's a question which can't be answered, befitting this holiday season-- "do you hear what I hear?" Even though my ears will (barring any specific deficiency) receive and transmit to the brain the exact same frequency information as yours will, there's simply no way between us to know if even a simple sine wave causes an identical psychological sensation. And, once you get into complex sounds, there's the "cocktail party effect" which I've talked about before-- you hear what part of the sound you decide to attend to, and two observers presented with the same sound stimulus can have a completely different experience.
And yet, we all hear pitch. The fact of pitch is invariant. An F is an F is an F; regardless of whether you intuitively recognize where it is placed in the musical scale relative to any other tones, you will recognize a pitch to be the same whether you hear it produced by a piano, a flute, or a bandsaw. Somehow, when we hear a single complex tone, our minds apply an extraction process to retrieve its essential identity as a pitch. Why pitch-- and, more pointedly, why a pitch? Why does a great mess of overtones always appear to our ears as a single recognizable and quantifiable (if not identifiable) sensation? It's not that we simply hear the most prominent frequency, into which our mind folds the overtones as texture; there's the "missing fundamental" phenomenon in which we hear a tone which isn't even there, and "the pitch may not be the first partial... the hum tone of a bell is not the pitch to which the bell is tuned."
I'm curious, of course, to know how this contrasts or complements my previous speculation of pitch as a reflexive, primal response to sound. It's still true that if you're made aware of any particular overtone you can hear it as separate from the rest of the complex tone. Pitch extraction doesn't necessarily depend on the entire tone. If I wanted to be stubborn-- if I wanted to cling to the supposition that I was right-- I'd consider the possibility that the person with perfect pitch begins, as a child, with the raw sensation of frequency-as-pitch, and learns through life experience to associate that same sensation with more complex tones; but I don't have any science to back that up, so for the moment I'll simply have to shrug and see what Nering tells us about the history of pitch perception research.
She begins with a citation from an out-of-print book, from an article within that book by Frederic Wightman:
[Wightman] divides the history [of pitch perception research] into 3 distinct periods which seem to be related to the dimensions of pitch. The first period, starting in about 1840 and lasting until about 1940, was characterized by the first systematic studies of pitch perception and the consequent "place" theory. The second period, from about 1940 to 1970... developed what is sometimes called "fine-structure" theory. ...A new theory began to emerge around 1970, described as "pattern-recognition" theory.
What I find extraordinary about this section of her thesis (you may have already inferred this yourself) is that I'm suddenly presented with the difference between pitch reception and pitch perception, which until this point I'd been treating as essentially the same thing. Despite the fact that over the past couple of weeks I'd accepted that pitch analysis happens in the mind, not the ear, I hadn't really considered the fact that, therefore, it's not enough to simply recognize that the ear transmits frequencies to the brain to create the sensation of pitch. Once the frequency impulses arrive in the brain, some recognition process occurs to extract the pitch from the torrent of simultaneous information. Egad... my mind boggles with all the potential consequences of this notion (given that tonight I have a finite amount of time to write about it!). Perhaps the most interesting fact which immediately occurs to me is that both a piano tone and a sine wave of 440 Hz are distinctly, perceptibly "A". Whatever pattern may be recognized, it must be applicable on many different levels!
I've been misapprehending that "place theory" describes how we perceive pitch. Vorarbeiten von Seebeck is credited with the first serious study of sound perception as frequency analysis, in 1841. Apparently, no less a mind than G.S. Ohm (yes, that Ohm) suggested, two years later, that complex sounds are filtered into frequencies. Helmholtz joined that wagon with the idea of the ear as spectral analyzer-- to accomplish this filtering-- and von Bekesy proved it. However, despite the illumination that place theory provides to the function of the ear, and despite place theory's critical importance to the physiological reception of pitch, place theory doesn't explain pitch perception. It was Seebeck himself who demonstrated the missing-fundamental effect, yet place theory persisted as the explanation of perception-- and, as is probably evident from what you've read on this site, it continues to persist, because the distinction between pitch reception and perception is rarely drawn except by those who are studying the subject in depth; and even those who are don't typically bother to mention the difference, merely representing (for the sake of convenience?) the simple fact that pitches are perceived.
Place theory was finally unseated by fine-structure theory; this theory suggests an "autocorrelation" in which the mind combines and calculates the received frequencies into perceived pitches. If you've tested out some of the sound files I've recently posted you're directly aware that this does occur; however, Nering says that the principal failing of fine-structure theory was its assumption of a direct mathematical interaction of frequencies. Not only can pitch be perceived when the harmonics are presented to the ears separately, but also:
Patterson showed in 1973 that scrambling the starting phases of the harmonics of a complex tone can dramatically alter the fine structure of the stimulus wave form, yet it will not affect the pitch in any serious way. (Nering doesn't seem to include the citation for this "Patterson" reference.)
Which leads us to pattern-recognition theory, in which "the auditory system somehow finds the best-fitting harmonic template." If you want one flavor of pattern-recognition theory straight from the horse's mouth, Ernst Terhardt has an explicit academic description of his theory available for you to read. His "learning-matrix" virtual-pitch theory explains pitch perception as a learned phenomenon, and resolves the apparent contradiction between "spectral pitch" (determined by the specific sound frequency) and "virtual pitch" (determined by the arrangement of overtones) by suggesting that, having learned the aural shape accompanying the spectral pitch, our minds can apply closure to situations in which certain aspects of the shape are missing, in the same way that our eyes can create contours of shapes which are not there.

Presumably, if you hadn't learned what a triangle looked like, you wouldn't see a triangle in this shape; but since you have learned, your eyes insist that there is a triangle there. The only way you can't see a triangle is by forcing yourself to ignore one or two of the red pac-men in this picture. Terhardt claims your ear will, according to this same principle, automatically interpret a missing pitch from the shape of that pitch implied by harmonically-related tones. (I'm already wondering how Mathieu's observations will support or detract from this theory.)
According to Nering, two other scientists came up with strikingly similar explanations at about the same time. A guy named Goldstein invented "optimum processor" theory, in which the mind doesn't rely on the direct mathematical interaction demanded by fine-structure but instead infers the most appropriate pitch based on the pattern presented. According to an article by Mike Taylor ("Modeling pitch reception with adaptive resonance theory", from Connection Science Jan 1994, which had been on-line but has been removed since I wrote this entry),
Goldstein includes a hypothetical neural network called the 'optimum-processor', which finds the best-fitting harmonic template for the spectral patterns supplied by its peripheral frequency analyzer. The fundamental frequency is obtained in a maximum-likelihood way by calculating the number of harmonics which match the stored harmonic template for each pitch and then choosing the winner. The winning harmonic template corresponds to the perceived pitch.
The difference between Goldstein's and Terhardt's theories seems to be that Goldstein wouldn't require that the original "shape" have been learned before the mind is able to comprehend it. I'm not sure whether I'm missing something, here, but that would seem to imply that Goldstein assumes that the brain has a "frequency analyzer" which is genetically designed to perceive pitches. Note to you geneticists: that's perceive pitches, not identify pitches.
I'll also use the Taylor paper to explain the pattern-recognition theory put forth by Wightman, because its explanation is succinct:
It was inspired by what appears to be a close similarity between pitch perception and other classic pattern-recognition problems. In his analogy between pitch and character recognition, he describes characters as having a certain characteristic about them, regardless of size, orientation, type style etc. For example the letter C as it is seen here, has its C-ness in common with other Cs, whether it is written by hand, printed in a newspaper or anywhere else. Even though the letter style can vary greatly it is still recognized as the letter C. Wightman argues that in music this is also true, e.g. middle C has the same pitch regardless of the instrument which produces it. Hence, he concluded that the perception of pitch is a pattern-recognition problem.
So what's the most likely answer-- is it any of these theories? I found a rather poorly-formatted page which nonetheless contains substantial, if concise, analysis, including this devastating conclusion:
Notice, first, that successive investigators have chased the "location" of pitch perception farther and farther up the inner ear and into the brain, until today there's no "location" at all other than a large set of ganglia spread throughout the Sylvian fissure. Second, notice that each era described pitch perception in terms of the highest technology then available: in 400 B.C., a vibrating drum, in the 1840s a mechanical Fourier transformer, in the 1940s a time-based electronic autocorrelator, in the 1970s a complex computer program operating as a "central processor," in the 1990s a highly parallel neural net.
You mustn't take this to mean that pattern-recognition theories are ultimately wrong; at worst, they are merely incomplete. You can see that each era's description of hearing does accurately and correctly represent some portion of the process. It therefore seems reasonable to presume that we can apply the precepts of pattern-recognition theory to learning perfect pitch (which is what this all about, remember?), even if some day in the future pattern-recognition will be superceded by some more sophisticated understanding (as it may already have been, if the above quote's implication is on target).
These three scientists all agree that our minds will somehow extract a "C" (or any other pitch) from varying combinations of complex tones. Terhardt says that the complex pattern reinforces a learned spectral comprehension; Goldstein asserts that the pattern implies a genetically built-in spectral recognition; Wightman suspects that the overall pattern somehow is the pitch. So, to accommodate Goldstein, we do our best to get in touch with the spectral comprehension that our minds are coded to comprehend (this would, most likely, fall in line with the dehabituation idea I concocted earlier). To manage Terhardt, we make ourselves consciously aware of the result of each individual mental inference, and, deferent to Wightman, we should accommodate multiple instruments in doing perfect-pitch exercises.
I've concluded my discussion of Nering's section on "physical pitch", and coming up is what she has to say about "musical pitch". Before that moment, though, I'll draw your attention again to the almost rhetorical question: why is pitch-- and specifically, a pitch instead of multiple pitches-- evident to our ears from any given sound? (And, yes, I could have said "evident to our minds", but if I start making that kind of semantic distinction I'll trip myself up endlessly. When it's critical to note a process taking place in the brain, I'll say so, and likewise the ears; otherwise I'll just say what I mean, and you'll have to write to me if you feel offended by my linguistic imprecision.)
Just take a moment to listen to any of the sounds in your environment-- make some, if you like, by striking your hands or feet against things, or bouncing in your chair-- and you will hear a distinct pitch. You hear only a single pitch from any given movement, unless, of course, the movement is actually a system of multiple objects moving together (like a laser printer, perhaps). The click of the light switch when I turn it on, the whir of my computer fan, the thud of each footfall on the concrete outside my apartment, even the tickity-tick of the keys as I type-- in each, despite the fact that they are complex sounds, one and only one pitch brings itself out to my ear.
I mention all this principally because Nering begins her section on musical pitch with a curiously strident statement:
Perfect pitch ability is meaningless if one can't apply it to music, which is a human development.
The only external support she offers for this remarkably potent opinion is another, lengthier quote from Frank Howes, which merely says that music has nothing to do with biological or physical function, but is instead "expression of the human soul". Well, that may indeed be so-- it's a pretty idea, and I haven't the resources nor the inclination to seriously contest it-- but as Miyazaki has been careful enough to research, perfect pitch doesn't necessarily have anything to do with music!
It occurs to me that the various explanations of pattern-recognition theory seem to support the notion that language is predicated on simple pitch concepts; regardless of how the pattern is recognized, we know a linguistic sound for what it is the instant that it's created. I defy you to speak any phoneme distinctly and have your hearer fail to write down its corresponding alphabetic equivalent-- provided, of course, that they are familiar with your dialect. I think about the fact that over the telephone-- the device which inspired von Bekesy to his experiments-- lower frequencies are eliminated altogether, and it is over the phone that people often hear my name as Arusso instead of Aruffo. The telephone changes the pattern to the extent that the two sounds, spoken clearly but casually, are practically indistinguishable.
Nering's initial assertion seems strange to me. Nobody knows what makes perfect pitch "meaningful". Absolute pitch could be related to language, or movement, or spatial comprehension, or even an emotional awareness. The fact that absolute pitch is a hearing phenomenon naturally makes it evident in the practice and performance of music, but that doesn't mean it exists only for music. I suspect that, since Nering's study is dedicated to the understanding of perfect pitch in a musical context, and there really isn't much out there to make her think otherwise (except Miyazaki, whose research appeared afterward), it may not have occurred to her to consider that absolute pitch would have any relevance in a non-musical context, but I don't know for sure.
Nering's section about musical pitch is, more than anything else, a brief history of music. The perspective she intends to illustrate is that of the developing role of pitch in music. It is curious that she begins the section by saying that perfect pitch is meaningless without music, but then immediately follows that with the statement that, initially, music had nothing to do with absolute pitch, only relative pitch. She does refer to Frank Howes again to assert that "the first music in any culture is singing, which grows out of the spoken language," but doesn't wonder why language preceded music, or if absolute pitch then had any application in language.
I'd better make the point once, and stop harping on it-- Nering appears to be convinced that absolute pitch is a musical ability. Furthermore, it appears at first glance that she's bought into the same conclusion I've seen elsewhere, which is that a listener's absolute pitch perception is somehow dependent on the musical scale. Just a quick analogy should make clear how that's not quite so-- if you saw swatches both of turquoise and of an ordinary blue, but you had no word for turquoise, you would perceive quite clearly that they were both substantially different color experiences, but you would name them both "blue". What you say is dependent on the "color scale", but what you perceive most definitely is not. It's been made clear to me, in communications from those who have perfect pitch, that the musical scale is useful mainly as a series of touch-points, as convenient "baskets" into which groups of pitches can be categorized. The musical scale is used as secondary reference-- the end point, not the base. In learning perfect pitch, we approach the process backwards, because these are the sounds we are already the most familiar with.
I've been asked a few times how I've been coming along in my own effort to learn perfect pitch. I was very satisfied the other day when, completely cold, I approached one of the exercises and aced it on the first try, without even one error. This was the exercise of naming C, D, E, or F (twenty in a row). Still, I'm concerned, because I don't know for sure if this means that I've begun to listen to sounds absolutely or if I'm instead memorizing the sound of the piano pitches. I suspect that I'm at least coming closer to listening absolutely; I was startled last week when I realized that, in listening to one note played after another, I had begun to listen to them as separate harmonic events rather than a "low note" and a "high note" in a single interval. That's definitely the right way to go.
To give you a sense of what Nering's section on musical pitch will discuss-- have you ever thought about the fact that there are only twelve tones in the scale? Perhaps you know a bit of the history of the musical scale, and about the establishment of "equal temperament"; but I wonder if you've stopped to consider that you can play an A-natural at 440Hz, or an A-sharp at 466Hz-- but if you play anything in between it's not only nameless, but wrong. Although there is some use to these middle notes, I'm told, in blues and in jazz, for the most part they are ignored or disallowed.
Why do we exclude literally thousands of sound frequencies from music?
There's not too much I want to say about this section on musical pitch. Maybe it's because I seem to have already encountered all of its information in various forms in my earlier explorations around the web. So rather than attempt to summarize the section, I can point you to a few different sites and let you read on if you wish. The main literal point is that musical scales can be explained by mathematical ratios of consonance and dissonance, and as music became gradually more complex it became more necessary to have a scale of fixed pitches:
...with the introduction of harmony... it put a premium on the scale offering the largest choice of concordant intervals. Harmony emphasized tonality and all notes were related to the tonic.
This offers an answer to the question that I posed in my last entry; we exclude thousands of pitches from our musical scale because, mathematically, they have a weaker relationship to the tonic. This doesn't explain why we eventually chose the pitches which we have for our existing pitch structure (that is, why a concert A is 440Hz instead of anything else) but at least, when you read about the Pythagorean scale, it shows why a scale stops at twelve tones. The Pythagorean scale was followed by just intonation and then by the most commonly used scale of equal temperament.
The development of fixed scales reminds me of clocks. I realized the other month that international time zones must be a fairly recent invention. After all, I considered, until the development of worldwide communication, time zones would be utterly irrelevant-- after all, it wouldn't be important to know that New York is "three hours ahead" of California if any communication between the two locations would take weeks or months to complete. And sure enough, I discovered that it wasn't until the advent of the cross-continental railroads, which required coordination over long distances, that time zones were even considered. I learned that the current system wasn't proposed internationally until 1884, and wasn't officially established until as late as 1918! Before then, time was a purely local affair, and residents would synchronize their watches to some publicly visible clock (why do you suppose so many town halls have a giant clock on their roof-- remember Back to the Future?). If you didn't need to share your music with anyone else, why would you have any greater need for fixed pitch than you did for fixed time?
"Concert A", currently fixed at 440Hz, has in fact ranged all over the place until very recently. The most comprehensive history of musical pitch appears to be a paper called The History of Musical Pitch, by Alexander Ellis, which, despite its purported significance and despite its being presented in 1880 (and therefore, presumably, now in the public domain) doesn't seem to have been reprinted anywhere on the web. If someone can send me a link to it I'd appreciate it. Nering refers to Ellis' paper in saying:
Pitches for A4 amazingly ranged from 373.1 Hz, that is F# today, found in Paris on Delezenne's 1854 foot pipe, to 567.3 Hz, a sharp C# today, found in North Germany on an old Praetorius church organ.
So... does musical pitch have any relevance to learning perfect pitch?
If there's any point in musical pitch which bears on learning perfect pitch, it seems to be the fact that musical scales group notes into categories, which makes the sound easier for the human mind to comprehend.
Nering offers some speculations about how perfect pitch may have been "useless" until the advent of a fixed-pitch system, because the pitches selected weren't from a consistent scale, but perhaps if she'd talked to that Japanese lecturer she'd have suggested instead that a person with perfect pitch would still have the advantage of being able to feel the harmony of each newly-introduced sound more clearly than someone who has only normal relative hearing. In any case, neither her suggestions nor mine have any kind of historical support readily available, but are instead predicated on our individual understanding of what perfect pitch is, so I'm quite content to leave that debate right where it is.
As for the musical scale in learning perfect pitch-- why are the categories important? I think I'm beginning to understand that, partly from inference and partly from my own experience. The musical scale gives us (the learning listener) two advantages: a discrete and consistent catalog of sounds which is constantly reinforced by our continuing musical experience, plus the explicit recognition that these twelve sounds are all significantly and recognizably different from each other.
Regardless of the influence of timbre, learning each of the twelve scalar notes individually is like establishing a series of stepping stones. Because all twelve tones are determinably different to our ear, we are able to learn twelve separate sound sensations. Then, as we become more and more familiar with each of these sensations, we should begin to think to ourselves, that can't be a G, because if it were it would sound more G-like-- this, as opposed to bluntly and consciously comparing the note we hear to some "reference template" which gives us the answer by process of elimination. That is, rather than make a quantum comparison between sensation G and sensation F, we can feel how a G is not like an F and, gradually, begin to feel the G-ness or the F-ness of a sound regardless of where it actually falls on the scale. Bit by bit, we would build a perceptual bridge between each pitch. I suppose another way to think of it would be to imagine twelve poles and that we're gradually drawing up the rope between them in order to walk across continuously. Eh. Metaphors have a tendency to get silly and overwrought, so enough of that. Enough to say that I express this because, in some limited ways, this is how I've begun to be able to recognize the C and the F.
I love optical illusions. I can remember enjoying them ever since, as a kindergartener, I read The Wizard of Op at my elementary school library.
Now and then I'll search the web for new optical illusions-- usually the websites that I find merely repeat the ones I'm already completely familiar with (and you probably are, too), but every so often I'll stumble across one I hadn't seen before, and that's always a delight. I was stunned when I came upon this, which is possibly the best example of its kind I've ever seen:

Squares A and B are the same shade of grey.
I sincerely doubt that, no matter how closely you look at this, you will be able to see these two greys as identical. I was so amazed that I cropped the picture to leave just the two squares:

but even then, they still didn't look exactly the same. It wasn't until I overlapped them
![]()
that I was able to definitely see them for what they were. This is, of course, a perfect example of how our minds infer perception based on the context of what our senses receive; and I don't just mean the shades of grey. Answer honestly: when I said that "the grey squares are the same shade", did you say to yourself that's not a square, that's a parallelogram? Two-dimensional perspective is as much a trick of the mind as the illusion itself.
At some time in your life you must have encountered the faces-as-vases illusion. It's very difficult to see both the vase and the faces at once. It is possible to perceive the other with your peripheral vision-- but only if you tell yourself that one of the figures is behind the other. Until you directly and deliberately concentrate on that idea of their being superimposed on each other, you'll only see one (and even then it's not easy).
There's an explanation for that-- a marvelous explanation (with my emphasis):
Perception is not determined simply by the stimulus patterns; rather it is a dynamic searching for the best interpretation of the available data. ...[P]erception involves going beyond the immediately given evidence of the senses: this evidence is assessed on many grounds and generally we make the best bet... [b]ut the senses do not give us a picture of the world directly; rather they provide evidence for the checking of hypotheses about what lies before us.
Based on this conclusion about sensual perception-- which looks like it could've been lifted right out of Terhardt's playbook about pattern recognition-- I confidently suggest that since all hearing takes place in the brain, psychologically, we can assume that the methods by which our brains interpret sound are identical to how we interpret vision. This perspective not only directly supports pattern-recognition theory, but it opens up a wider field of analogy, since we can theoretically apply principles of visual illusion and perception to aural perception as well. After all, if we grow up understanding that pitch is not "best interpretation of available data", but in fact that it is the worst, then it will never be learned.
It certainly could be for this reason that I had intense difficulty identifying pitches within intervals, and why I still struggle with them. Even when I ace an entire round of individual note identification (C, D, E, F, or G, naming 20 in a row without error), I can move on to intervals with only these same notes and blam! I can barely do two or three before I'm hung out to dry. My mind has been too well-convinced that the relationship of the notes to each other is the "best interpretation" of the sound I'm hearing. But, as the task is becoming easier-- "two or three" is better than the "none or one" that it used to be-- I'm gradually training myself not to think so.
At some point in the future I may want to explore parallels between visual illusions and aural illusions. The color-shading trick above seems similar to Shepard's endlessly-ascending scale, in which the listener can't tell what octave the note is in; more than one study confirms that octaves are perceptually analagous to color brightness. What other tricks of visual perception can be applied to sound comprehension? I have so far found at least one page which attempts to offer brief explanations of why each illusion fools us. If I understand more clearly why certain visual illusions affect us the way they do, I would be able to identify an aural equivalent.
All right! Now we're on to the section on perfect pitch. Something which I'll want to keep in mind, I suspect, is that Nering's paper is predicated on its analysis of the David Burge method-- so, despite whatever history or analysis she provides of absolute pitch, it's probably most important for her to illustrate Burge's definition.
I'm somewhat surprised to discover that the term "absolute pitch" is fairly recent, and was invented by a German, Karl Stumpf; in 1890 he named it "absolutas Gehör" (absolute ear). This is less surprising, of course, when you consider the fact that fixed musical pitch has only come into style just as recently. If there's no consensus about what to name a particular pitch sensation, identification becomes impossible and recall is irrelevant except to local pitch standards.
I'm intrigued and frustrated by the references that Nering cites in this section. Intrigued, because the titles, authors, and brief quotes make me think that I would learn much more from examining the publications; and frustrated because, of course, tracking down each one of them would be difficult. There's a peculiar incongruity in seeing all the professional scientific citations right alongside mention of David Burge's "handbook"; notwithstanding Burge's attempts to teach absolute pitch to his students, the "handbook" (which I've read) is David Burge's personal opinion, rather than anything scientifically tested and demonstrated.
She cites three publications that I'd like to read. One of these is, of course, Mark Rush's Ohio State dissertation. Another reference, which doesn't seem to be mentioned anywhere on the net, is Rita Steblin's Towards a History of Absolute Pitch Recognition, published in 1988; a third is an article from the Psychological Review from nearly a century earlier, in 1899, titled "Is the Memory of Absolute Pitch Capable of Development By Training?" This last article is cited by both Levitin and Miyazaki on-line, but it seems as though the article itself (despite being in the public domain) has not been reprinted electronically.
It does appear as though Nering's main interest is to use these other researchers as a reference for Burge's work. Rather than explain exhaustively the history of absolute pitch and its musical and scientific understanding, she relates each theory and hypothesis directly to Burge, and relies on historical research principally for ways to explain Burge's product.
Let me remind you of something. You already know how to recognize sounds instantly.
I don't just mean ordinary sounds which you perceive in your environment-- the click of a mouse, dishes falling to the floor, a door hinge squeaking-- but abstract sounds, which aren't intended to represent the physical movement of their source. For example, a musical pitch is an abstract sound; when we hear it we know we aren't meant to visualize the striking of hammers on xylophones, or the scraping of horsehair on catgut. We know we're supposed to interpret the sounds emotionally, not literally.
Language is also an abstract sound. When you hear language, you know you're supposed to interpret the sounds intellectually, not literally.
And you already know how to recognize spoken words instantly. You can recognize them spoken in different accents, at different pitches, with different speeds, and mixed with other sounds. You can't possibly hear a linguistic sound clearly-- in your own language-- and not recognize the phoneme it's intended to convey. Just take a moment, right now, to speak a few different nonsense sounds, and notice how quickly you comprehend the noise even when it doesn't mean anything. Splik, gref, merb, flemp. If you could just imagine for a moment that these sounds you're making aren't language, but pitches on some weird musical scale... well, now you know what it's like to hear with perfect pitch. In a fraction of a second you hear the nonsense syllable "gref" and, without even having to think about it, you know you've just heard "gr", "eh", and "f". In the same way, a person with absolute pitch hears a chord and immediately knows he's just heard D, F#, and B. Perfect pitch is that obvious, and that impossible not to hear.
But is language just as obvious? I was reading The Scientist in the Crib and was startled to see this anecdote on page 103:
Pat [one of the authors] was in Japan to test Japanese adults and their babies on the r-l distinction. She had carefully carried the computer disk with the r and l sounds to Japan, and when she arrived in the laboratory in Tokyo, she played them on a very expensive Yamaha loudspeaker. She thought that such clearly produced sounds would surely be distinguished by her Japanese colleagues, who were quite good English speakers as well as being professional speech scientists. As the words rake, rake, rake began to play out of the loudspeaker, Pat was relieved to know that the disk worked and that the sound was perfect. Then the train of words changed to an equally clear lake, lake, lake, and Pat and her American assistant smiled, looking expectantly at her Japanese colleagues. They were still anxiously straining to hear when the sound had changed. The shift from rake to lake had completely passed them by. Pat tried it over and over again, to no avail.
I find it difficult to imagine that any person on the planet would think for an instant that this distinction between R and L can't be learned, even at these adults' advanced age. It seems ludicrous that anyone would claim for even an instant that this lack of aural recognition is somehow genetically determined. And yet, this prejudice is near-universal for musical pitch. Somehow the vast majority of people-- even some PhD researchers-- are convinced that the distinction between notes A and B can't be learned unless you're genetically born to do it.
The Scientist in the Crib features something that few other sources have yet shown-- research involving children. I've complained before about how the available research seems only to focus on adults, when perfect pitch is obviously something that manifests itself at a very early age. The only explanation I've received from anyone about why this might be so was in an e-mail from Daniel Levitin, last year:
Doing the experiment you suggest isn't so simple because it would require the cooperation of lots of people who aren't as interested in AP as you and me. For example, if we were to try to teach the children AP at school, we'd have to get the school district to allow us to eat up some of the curriculum time -- not a trivial amount, either. Even just 10 minutes a week for a school year would be very difficult to obtain from any school. Not to mention it would eat up about a year of a researcher's time, and grants to do this sort of thing.
I'm left scratching my head-- if it's so difficult to get access to children, why was Crib author Andrew Meltzoff able to gain access to hospitals, with apparent ease, in order to examine and test babies who were literally minutes old? How could the Crib scientists consistently examine and test children from ages zero to five? In Crib, the authors mention their own perplexity that so many studies and hypotheses have been created, about how children think and learn, without actually examining the children directly. The only conclusion I can draw at the moment is that Levitin makes the right point in that people "aren't as interested in AP" as they are in language and learning, which is what the Crib authors were researching. Perhaps Meltzoff and his partners were able to gain greater access to children because the parents of the children involved were more easily convinced that there would be some benefit to their children's intelligence.
I'm pleased that their research had such a strong emphasis on linguistic comprehension, though, because of the obvious parallels between language comprehension and absolute pitch. They cite direct evidence that children can unlearn the significance of certain sounds, and be trained instead to make different associations.
Scientists anticipated... that very young babies initially can't hear the subtle differences between speech sounds and only slowly learn to distinguish those which are important in their particular language... in fact, the results were just the reverse. ..[S]hortly afterward speech scientists discovered something even more remarkable. Kikuyu babies in Africa and Spanish babies in Mexico were also excellent at discriminating Spanish sounds-- much better than American adults. ...Very young babies discriminated the sounds not only of their own language but of every language, including languages they had never heard. (p 105-106)
Japanese and American seven-month-olds discriminated r from l equally well. But just three months later... Japanese infants could no longer hear the change from r to l. American infants not only could do so but had actually gotten much better at making the distinction. (p 107)
How is this parallel to absolute pitch? Nering has tracked down a handful of studies which, although they don't examine children, do attempt to relate perfect pitch and early age. Here's the result of a survey conducted in 1969 by D. Sergeant. He asked musicians about what age they began their musical training, and observed the relationship between age of musical training and incidence of perfect pitch.
Does this look coincidental to you?
There's a logical trap here. You might be tempted to think that the occurrence of absolute pitch was due principally to the introduction of musical training at early ages, and that music induced absolute pitch. Let me point out to you that musical training, at present, is the only form of aural training in our culture outside of language. For comparison, think about the fact that kindergarteners may be treated to musical training in their normal curriculum, just by itself-- but irrespective of artistic training, they are separately taught their colors. Careful attention is devoted to children learning their colors, regardless of whether they indulge in fingerpaints, pastel pencils, or brush painting. Would you expect children to learn their colors if fingerpainting was the only visual education they were given? And it's incredible how much science, theory, and attention is devoted to the effort of teaching colors. Does this have anything to do with "artistic training"? Of course not. Nobody that I'm aware of has developed a broad attempt to teach aural comprehension outside of musical training.
Even so, I'm not the first person to think this. According to Nering, it has been done, sporadically; a man last name of Abraham (Nering really doesn't like including first names, for some reason) "in 1901 found that pitch-naming ability was relatively easy to develop in children." In 1980 Natasha Spender wondered, just as I do, if it would not be possible for children to learn pitches at the same age as their colors. Nering quotes Spender's speculation:
If innate endowment plays a negligible part, then absolute pitch may be attributable to environmental good luck in being provided with verbal labels when attention to sensory experience is uppermost, before the habit of ignoring sound quality has been thoroughly learned. Ease of acquisition depends on its being established before concentration on "symbolic" cognition removes the focus of attention away from sensory experience.
A valid speculation, but how does it relate to aural comprehension of language? Is phoneme discrimination a sensory experience or a cognitive one? Consider again the Japanese scientists who can't tell the difference between R and L. Just consider, off the top of your head, how you personally would begin teaching these adults how to recognize the difference.
What would you do? Would you ask them to "feel" the emotional difference between these two sounds? Or would you just play the two sounds for them over and over again until they "got it"? Or something else entirely?
Yesterday I was walking through a grocery store and noticed that the store's paging system played a tone before each announcement. Bing! --Jennifer to the register, please, or Bing!-- Cleanup on aisle 6. The tone sounded familiar to me, so I searched my memory for the piano tone which matched it. And I found it. E. Good old plain old E. This, although encouraging, is still too slow. I could understand "Jennifer to the register, please" as it was being spoken, but it took me a good half-minute to identify that E.
Peter managed to teach himself absolute pitch by listening to the pitches as though they were vowel sounds. Although my own experiments have shown that the direct relationships of vowels to pitches is variable, the fact that he was not listening for a musical sound seems to be the critical factor. Regardless of which vowels he associated with each sound, he instantly recognized some inherent quality of each despite, not because of, their musical identity.
Although I am continuing my own ear-training practices and I fully expect it to yield results, I am beginning to think that there must be some way to accomplish pitch training divorced from a musical context. The Crib authors propose a solution to the Japanese r-l problem: they say that the sounds should be repeated over and over, but "exaggerating the differences" between the sounds. How do you most effectively exaggerate the differences between pitches? Manipulate the overtones? Play one tone louder than another? Play them on different instruments? Work with spoken (or whispered) language sounds instead of musical instruments?
I may have found a clue in a book I've been reading called Eye and Brain: the Psychology of Seeing. Its parallels of visual perception to aural perception are immensely clear. On page 85 of the 1976 edition, I read
One of the oldest laws in experimental psychology is Weber's Law. This states that the smallest difference in intensity which can be detected is directly proportional to the background intensity. For example: if we light a candle in a brightly lit room, its effect is scarcely noticeable, but if the room be dim to start with-- say, lit by just a few other candles-- then the added candle makes a marked difference.
There must be some way to translate this effect to absolute pitch training, and thereby exaggerate the differences between pitches.
Children may pick up absolute pitch naturally within musical training, but it may be necessary for adults to take it out of that context. There are other aspects of learning and memory which I'm going to have to address as I develop a more meaningful curriculum-- and I don't just mean taking advantage of the brain's ability to hold more information in its short-term memory when the information is presented along multiple dimensions. If you've read enough of my website, I'll be surprised if you still "believe" that absolute pitch is something which is genetically endowed, and not a natural perception which is culturally inhibited. I dearly hope others with scientific knowledge of education will take up the torch and begin thinking of ways to teach children pitch recognition outside of a musical context. I would love to see the day when pitch training is offered right alongside color training in every school, and is considered equally important.
Why, you ask, would anyone want to teach their kids pitch recognition? Well I'll tell you honestly: I don't know.
How could I know? Except for possible advantages in musical performance and composition, right now nobody knows. How could we, when only one in ten thousand people exhibits perfect pitch acuity? People argue that color recognition is a natural thing to be taught because "there are colors all around us" and because "we use colors in our everyday life" which we need to recognize in order to get by, such as the difference between the customs and insurance forms at the post office. But sounds suffuse our daily life just as surely as colors. We create designs which rely on color discrimination because we are able to discriminate colors, not the other way around. Why does it matter what color your shoe is? Why would the color of wallpaper be important? Pragmatically, it doesn't matter a bit that we can call one "blue" and another "red"-- and I'd suspect that any examples you can think of, which make it essential for you to know color, have been manufactured by humans.
I've come across the occasional article which explains, with some interest, the fact that the current generation of children has become the "thumb generation". The most obvious observable effect is that they use their thumbs for tasks which are, historically, executed by the forefinger. This is because they are being trained to use their thumbs in ways which previous generations never had the opportunity to try; the results in their daily lives are surprising when they appear, but nonetheless easy to understand.
So if we raise a generation of children who all have absolute pitch acuity, if we give an entire generation an ability which we've never had the chance to experiment with ourselves on a broad cultural scale, who knows what kinds of purposes they'd put it to? I'm sure I don't know-- but considering all the ways that color discrimination does in fact impinge on my own life, I'd love to find out.
I've been interested in returning to the correlation of vowel sounds to pitches. This is mainly because of my most recent entries, which draw a very direct relationship between the way we perceive language sounds and the way we learn (or don't learn) musical sounds-- but it's also because I've been having limited success in my exercises over the last week. I seem to find time for exercises only when I'm already exhausted or stressed out, and as you might imagine it's difficult to accurately identify subtle emotional experiences when you're thoroughly drained. I figured it'd be best for me to listen for the vowel sounds instead.
So, tired as I was, I booted the program, played a note, and I forgot to listen for the vowel. Still, it sounded like a low G. But I promised myself I'd try the vowels, so I gamely played it again and this time heard, with startling clarity, the a as in father. That can't be right, I thought-- if it were a G, it would be i as in bit. A-as-in-father is what I'd hear from F, not a G. I played it three more times and listened for the vowel; it was undeniably, obviously, the a sound of father. I played it a fourth time, listening to it emotionally, and it still sounded G-like. Oh well. My whisper-recordings had shown that the vowel relationships weren't exact anyway. I guess this G must sound like an a sound. So I pressed the Note key to show me what note it was.
And it was an F.
Nering begins her section on absolute pitch by discussing what people claim it means to hear in perfect pitch. Her sources generally agree that each pitch has a distinctive sound to it which is "instantaneously recognized and never confused" (that quote's from Natasha Spender). Nering refers to experiments conducted by Karl Stumpf, in the late 1800s, in which he determined that he and other perfect pitch listeners did indeed listen for unique qualities of the individual pitches. This idea, surprisingly, was even then centuries old; Nering quotes a 1719 publication by a Mr Matheson:
Each tone that is set as the key-note of a mode possesses in itself, as a sound, such individual characteristics which distinguish it completely from all other sounds and imbue it with a totally different art, figure, name, strength, and nature.
Nering calls this identifiable characteristic "pitch color", and listening for this quality is what she refers to as "color hearing". Although I still don't like these terms, I nonetheless agree that the qualities must be named and recognized for what they are. Furthermore, I concur in dismissing the idea of "bi-dimensional" pitch, which suggests that a pitch is accurately represented only when its octave is included as part of its identity. As I've explained in the secret of lesson one, people with perfect pitch tell me that octaves are essentially an illusion which has been invented for musical convenience. Mathieu even suggests that, harmonically, the first note which should follow C is not D at all, but C's strongest partial, G. No-- the "octave height" of a pitch is ultimately secondary to its identity. However, it is precisely because the popular definition of "pitch" incorporates the octave height of a tone that it seems necessary to use the term "color" to describe a pitch. It seems clear to me that the analogy of pitch:sound should be the same as color:vision, flavor:taste, and scent:smell, but the term "pitch" has so many centuries of abuse that I fear I fight a losing battle against the extra word "color". Well, we'll see.
In any case, what is this "unique characteristic"-- what is the "color" of the pitch? How do we hear it? What are we listening for? This is what I've been thinking most carefully about for the past two weeks. The exercises presented in the product are the ones that the author himself used to learn perfect pitch-- but, as he tells you himself, he heard a form of "pitch color" long before he used these exercises to train himself to identify notes. We can't be sure that, by using these exercises, we will learn to hear "pitch color" in the same way that he hears it. All his explanations aim to help you make that spiritual, emotional connection to the sensation and feeling of the pitch. When your emotional state is taxed or off-balance, this method of recognition is unreliable-- and furthermore, it is possible to recognize a musical pitch as simply and clearly as a linguistic phoneme (specifically, a vowel) despite your emotional relationship to the pitch.
So when we attempt to hear "pitch color"-- the sensation of each individual note-- are we really trying to validate a spiritual connection with some heretofore-unquantified emotion, or are we simply trying to recognize something as intellectually straightforward as a spoken letter? It's my suspicion that the goal of perfect pitch training is to reach the latter type of recognition, and that the path to reaching it may begin with the former. At some point I expect to begin looking at the methods by which children are taught visual colors in order to learn the principles of color instruction, and apply those principles to learning pitch color.
Is perfect pitch of any use? Now that Nering has taken a cursory stab at what it is, she takes a moment to illustrate why it is. I've already found a brief, inspiring description which is worth a look.
Although Miyazaki is the only person I've seen who blatantly refers to absolute pitch as an inability, Nering interviewed Lois Chosky, a music instructor with 20 years' experience, at the University of Calgary, and declared
[Chosky] has found there exists a kind of perfect pitch ability which is a detriment to musicianship, whereby a possessor hears pitches as individual unrelated phenomena. This type of person does well on pitch dictation exams, but has difficulty with such things as seeing patterns and relationships, thinking in melodic lines, and transposing. This type of perfect pitch is too rigid and locked in.
Nering hurriedly explains, though, even as I would, that it's entirely probable that this is not a "type" of perfect pitch at all, but represents a lack of relative pitch skills in the person tested.
I would like to see some of these studies which Nering has examined, though, because I have a suspicion that the scientific studies make only one distinction: possessors and non-possessors. I was fortunate to have read Miyazaki's full articles in English (he graciously provided me with them) and those are the two categories he uses. But there are definitely people with absolute pitch who have developed relative pitch; I've heard from one who says she "switches" into relative pitch listening when she needs to follow music quickly. I would recommend to the researchers categories which are not "levels of perfect pitch", but levels of musicianship. Are absolute pitch possessors really incapable of hearing the intervals between the notes, or are they simply untrained in the task?
I had initially speculated that people with perfect pitch were incapable of hearing intervals, but IronMan Mike disabused me of that notion. He (and Mathieu's book) helped me understand that he does hear an interval-- but he hears it harmonically. Rather than hear the "distance" between notes, he hears how they interact with each other, and that harmonic fusion is what he recognizes as "the interval". Miyazaki executed his test by making notes slightly out of tune and requiring his subjects to identify intervals based on those notes. Non-possessors scored significantly higher at this task than those with perfect pitch, presumably because they recognize and identify "distance" between notes. How would IronMan Mike have fared at this same test, I wonder? He is not only familiar with intervals, in his own way, but in his jazz improvisation he claims to be sensitive to intervals right down to the quarter tone. A quarter tone is the space between piano keys; it is half a semitone, or "50 cents" (where 100 cents is a full semitone). Since Mike speaks wonderingly about hearing in relative pitch, and shakes his head in amazement at what others tell him they hear in musical relationships-- and explains, in no uncertain terms, about how he uses absolute pitch to accomplish musical tasks which are typically relative-pitch tasks-- I'd be extremely interested to know how he'd score.
The mystery goes even deeper, though-- not just because of Mike's level of development, but because of what Nering describes of an experiment by Lola Cuddy. (Nering's description of Cuddy's experiment is itself second-hand, filtered through the opinion of Dixon Ward, so here I'm adding a fourth layer of noise.) Ward suggested that perfect pitch possessors "...are, it appears, less flexible, less able to learn a new scale," based on Cuddy's work, summarized here by Nering:
In 1977 [Cuddy] devised a study whereby possessors and non-possessors were to identify when two seven-tone melodies were identical or one of the tones differed by half a semitone. Possessors displayed superior skill at distinguishing tonal sequences in the logarithmic scale. They were better at picking out a single mistuned tone from a sequence, but when many of the tones were mistuned from the standard scale, they were unable to determine whether or not an additional 50 cent change had occurred.
This is similar to Miyazaki's experiment, but whether she intended it or not, Cuddy's approach has yielded a different result. Nering, after this description, suggests that Cuddy's result supports absolute pitch as a learned ability, because their understanding of pitch has clearly been pegged to arbitrary divisions of sound frequency. I suppose that's true enough; but, upon reading this passage, I immediately remembered this observation from The Scientist in the Crib (emphases are all mine):
Say we use the speech synthesizer again to change the sound b gradually and continuously to p, and we test speakers of many languages on these sounds. Americans will hear two sharp categories, b and p. Spanish and French listening to these same sounds hear two categories also but divide the continuous stream of sounds in a different place than the Americans do. What sounds like b to a Spanish speaker will sound like p to an English speaker. Thai speakers hear three categories. In each case listeners hear sharp changes-- quantum leaps-- between categories, with no in-between. But the speakers of Spanish, French, and Thai hear those quantum leaps at different places. And we English speakers don't even notice the categorical shifts Spanish or French or Thai speakers hear.
Cuddy's result, as reported by Nering, certainly seems similar to this effect. If the perfect pitch folk were listening to pitches in essentially the same way as linguistic sounds, then it seems only natural that they would be more attuned to the specific divisions of pitch, rather than the intervallic "distance" between the notes. Furthermore, if a note were already mistuned and then mistuned again, by less than a semitone each time, it's entirely possible that the absolute pitch listener would not hear the "quantum leap" from one pitch to another-- because to them the changes would be within the same category! The relative pitch listeners would, of course, be listening solely for a specific interval, attending only to "distance", and be indifferent to categories of pitch. Again, I wonder how IronMan Mike-- who has more "quantum" categories-- would do on a test like this.
[While I was writing that paragraph, just now, I did a quick Google search to see if I could find a link for you which would illustrate a fact I've encountered before: namely, that people with absolute pitch exhibit unusually strong activity in the same area of the brain that processes language. That area, the "left planum temporale", is often enlarged in those with absolute pitch. And I did find a link, very easily, and you should've seen me start with surprise when I read, on that page, that "scientists cannot explain why musicians should rely so heavily on a language-processing region of the brain." I wonder if that's still true-- that scientists can't explain it. If so, then you heard it here first, folks... the hypothesis that people with absolute pitch will mentally process pitches as though they were linguistic sounds. Perhaps I'll write to Takashi Ohnishi and suggest it to him.]
It also makes me realize that if absolute pitch is to be trained using linguistic sounds as a base, those sounds will not be consistent across cultures. The list of vowels that I developed with Peter's help might not translate to other English speakers who have different dialects-- and it's entirely possible that I haven't been able to hear all the vowels yet because, even though I was able to swap recordings with Peter to confirm which vowel sounds he heard, he (as a native Dutch speaker) may have different category boundaries even for vowels that he and I agree are the same.
Nering's conclusion from Cuddy's experiment is that "it seems possessors must suppress the tendency to categorize individual tones." I'm not sure they can "suppress" this, any more than you or I could suppress our ability to distinguish the letters a from p; and it's not clear if by saying this Nering is failing to infer that it might be possible to learn interval identities, irrespective of pitch categories, in addition to absolute pitch. Even so, I wonder if a person with perfect pitch would hear the intervals in the same way? ..well, I can't know that yet. There's the anecdotal evidence, though, of that musician who trained himself not to have perfect pitch any more-- I apologize for not finding the link again, but it's somewhere in the archives if you look-- and I wonder if that means that he was able to mentally void a linguistic understanding of the sounds. Hm.
Reading this section, I concur that absolute pitch will help a person perform music and listen to music-- that it will unquestionably improve one's musical life-- but absolute pitch is ultimately not necessary to musical success, because music as we now know it is inherently a construct of changing relationships. Nering finishes her section on the importance of absolute pitch with a couple of quotes that disparage absolute pitch. One author, John Davies, in 1978 saw no musical advantage to having perfect pitch. Dixon Ward referred to studies which illustrate absolute-pitch perception in animals and people with brain deficiencies in order to say, "It appears that absolute pitch is typical of either musical precociousness or mental retardation. So if you have it be sure it is for the right reason."